自动编码器一览（一）

发表于 更新于 分类于 阅读次数：

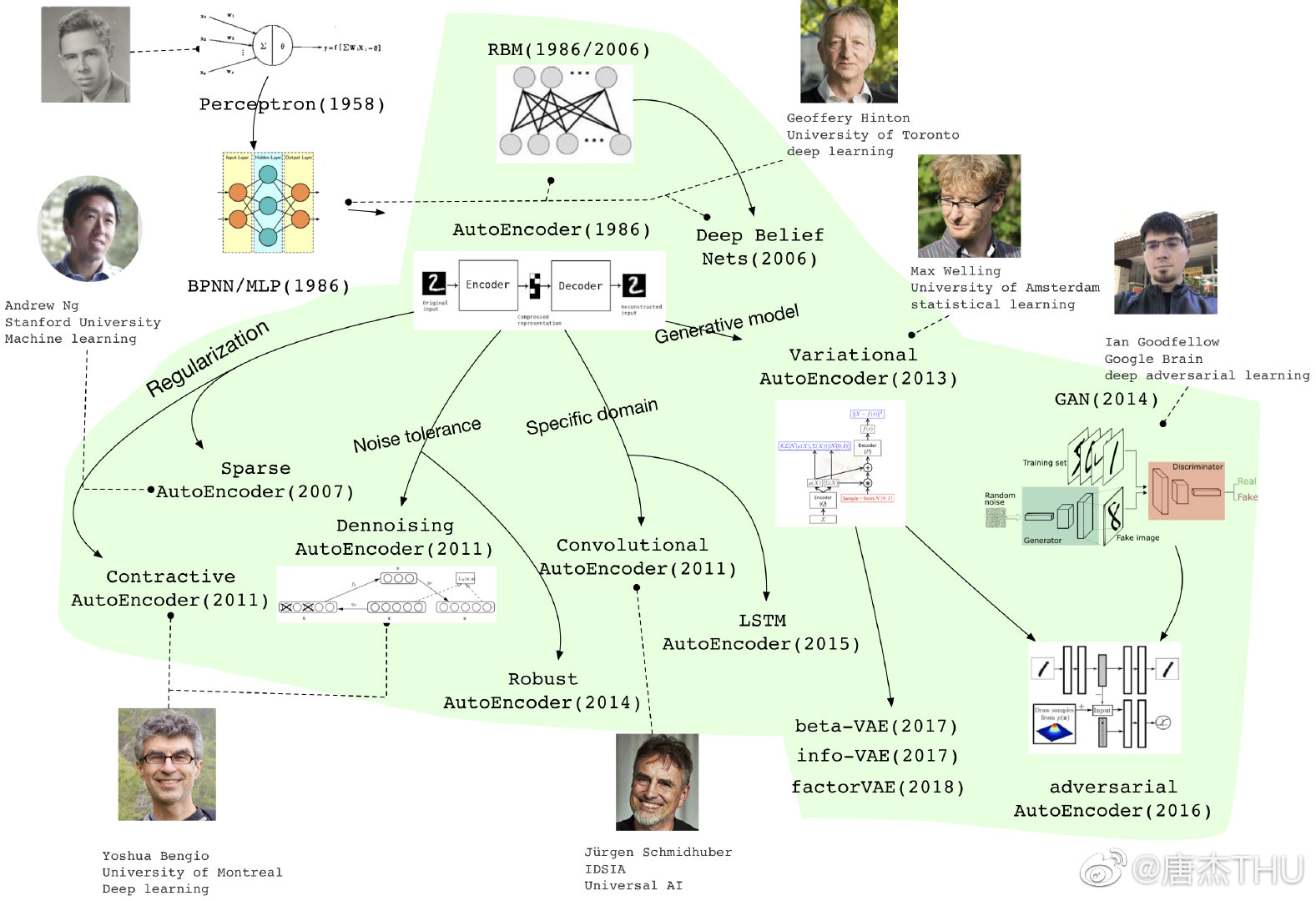
最近在研究用自动编码器（Autoencoder, AE）做表征学习（Representation Learning），看了一些资料和论文，自己也有一些想法，现在准备开始写 related work，值此机会想要先整理一下。题图来自 THU 唐杰老师的微博，清晰地展现了自动编码器的发展历程。

本系列预计会写三篇博文，第一篇包含自动编码器的总体框架和思想，之后介绍为实现各种目标而产生的一些经典变体，会涵盖题图中提到的大部分自动编码器；第二篇包含一些我个人比较感兴趣、最近看过的一些变形，它们更适用于各自的任务；第三篇可能会拖得稍微久一点，我想把最近非常火热的变分自动编码器以及它的一些变形弄通。

本文中包含以下内容：

  • 表征学习简介（Representation Learning Intro）
  • 自动编码器框架（Autoencoder Framework）
  • 堆叠自动编码器（Stacked Autoencoder）
  • 去噪自动编码器（Denoising Autoencoder, DAE）
  • 收缩自动编码器（Contractive AutoEncoder, CAE）
  • 稀疏自动编码器（Sparse Autoencoder）
  • LSTM 自动编码器（LSTM Autoencoder）
  • 卷积自动编码器（Convolutional Autoencoder）

“自动编码器一览”系列：

表征学习

在开始介绍自动编码器之前，我们首先对表征学习（Representation Learning，也称表示学习）做一个简单的介绍，帮助我们在之后更好地理解自动编码器架构设计的目的。

表征学习（或者称表示学习）指从原始数据中自动学习有效的特征（或者更一般性称为表征），并提高最终机器学习模型的性能。表征学习目前已经成为机器学习社区的热点之一，在每届 NIPS、ICML、ICLR 等会议都有较多的相关论文以及 workshops。

表征学习的关键是解决语义鸿沟（Semantic Gap）问题。语义鸿沟问题是指输入数据的底层特征和高层的语义信息之间的不一致性和差异性。比如图片分类任务，图片中每个物体的颜色和形状等属性都不尽相同，不同图片在像素级别上的表示（即底层特征）差异性也会非常大。人类理解这些图片是建立在比较抽象的高层语义概念上的，因此如果让一个分类模型直接建立在底层特征之上，会对模型的能力要求过高。如果有一个好的表示在某种程度上可以反映出数据的高层语义特征，那么我们就可以相对容易地构建后续的机器学习模型 [1]。

考虑到直接将高维度的原始数据输入到各类算法中会导致计算量非常大，因此，表征学习最大的目标之一就是在尽量保留对后续任务有用的信息的同时，对数据进行降维。比起进行线性降维的 PCA，自动编码器可以进行非线性的降维。同时，一个好的表征应该比较稀疏（用极可能少的资源表示尽可能多的信息，计算速度快）、对噪声不敏感（学习到的表征尽量不受原始数据中噪声的影响）、具有一般性，是任务或领域独立的（学习到的表征能够尽可能在更多任务上取得较好效果）、具有较好的可重构性、具有很强的表示能力（同样大小的向量可以表示更多信息）等等。

根据 [2] 所述，对表征学习的研究大致分为两类，一类基于概率图模型，另一类基于神经网络。这两类研究的根本区别在于，深度学习模型的层级结构被解释为对概率图模型的描述还是对计算图的描述。更简单地说，区别在于深度学习模型的隐藏单元是被视为潜在的随机变量还是计算节点。其中，自动编码器是后者的代表之一。

自动编码器框架

在这里，我们使用“自动编码器框架”来代指最基本的自动编码器架构和指导思想，以与单个自动编码器进行叙述上的区分。

自动编码器框架包含两个参数化函数。第一个函数 $f_{\theta}$ 称为编码器（encoder），它从原始输入 $x$ 中提取特征向量 $h = f_{\theta}(x)$。第二个函数 $g_{\theta}$ 称为解码器（decoder），它是一个从特征空间到输入空间的映射，产生一个重构（reconstruction） $r = g_{\theta}(h)$。通过让解码器产生的重构与作为输入的原始数据尽可能相似，即尝试在训练集上获得最小的重构损失 $L(x,r)$，编码器和解码器的参数组 $\theta$ 同时通过训练得到。具有较好泛化性意味着能够在测试集也取得较低的重构损失，而编码器所提取的特征向量即自动编码器框架学习得到的表征。

总结一下，自动编码器框架的训练目的是为了找到一组参数 $\theta$ 的值，使得重构损失最小。最经典的自动编码器使用多层感知器（Multi-Layer Perceptrons, MLPs）作为编码器和解码器，其常用的形式如下：

$$f_{\theta}(x) = s_f(Wx + b)$$

$$g_{\theta}(h) = s_g(W^{‘}h + b^{‘})$$

其中，$s_f$ 和 $s_g$ 是编码器和解码器所使用的激活函数，一般为非线性的 sigmoid、Relu 函数等。因此，模型整体的参数组 $\theta = { W, b, W^{‘}, b^{‘} }$，其中 $W$ 和 $W^{‘}$ 是编码器和解码器的权重矩阵，$b$ 和 $b^{‘}$ 是编码器和解码器的偏置向量。由于我们要求原始输入和输出尽可能相似，编码器和解码器可能最终被训练为恒等映射，不符合我们的要求，因此通常对表征做一定的约束。

由于自动编码器框架将原始输入同时作为模型的输入和输出，因此无需使用有标签的数据进行训练，这种无监督学习的方式使得自动编码器的通用性大为提升。其实早在 1988 年，自动编码器的思想就已经被提出，但是由于数据的稀疏高维，使得当时的模型很难优化，因此直到 2006 年，Hinton 采用梯度下降算法来逐层优化受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）以获得对原始样本的抽象表示并取得显著效果后，自动编码器才得到广泛的关注。

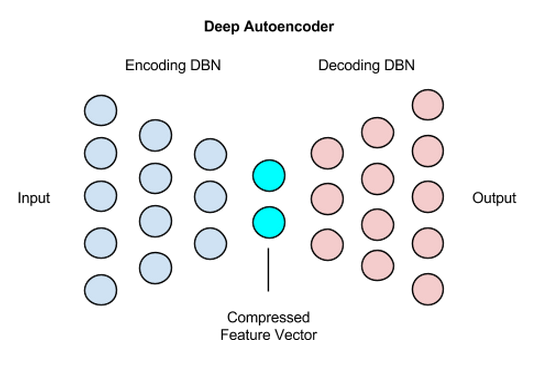
堆叠自动编码器

可以看到，最基本的自动编码器框架是一个简单的三层结构，包含输入层、隐藏层（中间层）和输出层。其中，输出层的存在是为了将原始数据作为假想的目标输出，以构建监督误差来训练整个网络。当训练结束后，我们就不再关心输出层，只关心从输入到中间层的映射。

考虑到深度神经网络是在逐层的学习数据的表征，在底层构建较为简单的特征，以此为基础在较高层构建更为复杂和抽象的表征，我们很容易想到，将最基本的自动编码器学习到的特征 $h$ 作为原始信息，再训练一个新的自动编码器，来得到新的特征表达。这就是论文 “Greedy Layer-Wise Training of Deep Networks” [3] 所提出的堆叠自动编码器（Stacked Autoencoder，又称栈式自动编码器）的基本思想。通过堆叠自动编码器学习到的高层表征更加抽象，具有更好的扩展性。

显然，堆叠自动编码器的训练和普通的多层神经网络不同，不是每一遍逐层进行，而是首先训练得到最底层的自动编码器，得到其编码器函数，然后再训练更高层的自动编码器，最后堆叠得到整个堆叠自动编码器。因此，除开进行无监督表征学习，堆叠自动编码器也可以用来进行深度神经网络的初始化，在通过无监督学习得到堆叠自动编码器后可以在最后一个隐藏层后，根据具体任务加上一个输出层，并通过监督学习的方式，利用梯度下降对整个模型进行全局微调。这就是逐层非监督预训练（layer-wise unsuperwised pre-training）。

去噪自动编码器

考虑到自动编码器框架中的编码器和解码器本质上还是神经网络，因此，当神经网络的层数加深、结构愈发复杂而使参数增加时，自动编码器一样面临着过拟合的风险。在 ICML 2008 上，论文 “Extracting and composing robust features with denoising autoencoders” [4] 首次提出去噪自动编码器（Denoising Autoencoder, DAE）模型。为了强制让隐藏层学习到更加健壮的特征，去噪自动编码器 DAE 在输入层对原始输入加入随机噪声。

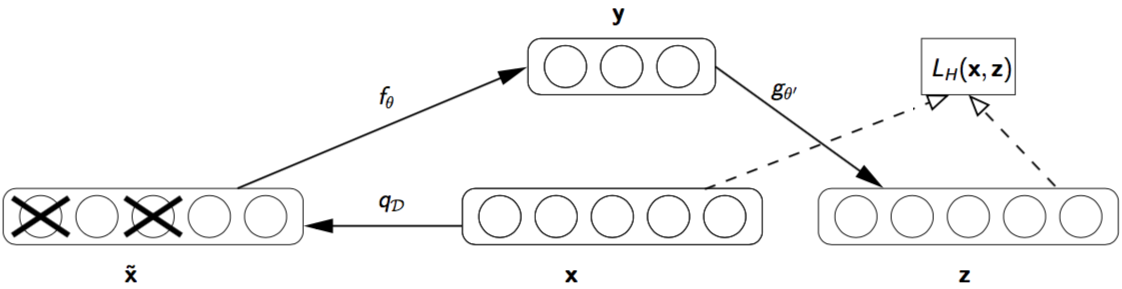
为了和图中符号匹配，请注意我们在本节中使用原论文 [4] 中的符号表示进行叙述，可能与前文中符号不同。去噪自动编码器 DAE 的描述如下：

  1. 设有纯净输入（clean input）$\mathbf{x} \in [0, 1]^d$，通过部分损坏纯净输入得到损坏输入（corrupted input）$\tilde{\mathbf{x}} \sim q_{\mathcal{D}}(\tilde{\mathbf{x}} | \mathbf{x})$。
  2. 原论文中的输入损坏过程 $q_{\mathcal{D}}(\tilde{\mathbf{x}} | \mathbf{x})$ 是随机选择纯净输入 $\mathbf{x}$ 中固定比例的一部分（一般不超过一半），将这些部分的值设置为 0。当然可以使用其他方法来损坏数据，例如引入高斯噪声。
  3. 编码器函数 $f_{\theta}$ 将损坏输入 $\tilde{\mathbf{x}}$ 映射到隐藏表征 $\mathbf{y} = f_{\theta}(\tilde{\mathbf{x}})$。
  4. 解码器函数 $g_{\theta^{‘}}$ 将 $\mathbf{y}$ 重构为 $\mathbf{z} = g_{\theta^{‘}}(\mathbf{y})$。
  5. 通过训练来最小化交叉熵重构损失 $L_{H}(\mathbf{x}, \mathbf{z})=-\sum_{k=1}^{d}\left[\mathbf{x}_{k} \log \mathbf{z}_{k}+\left(1-\mathbf{x}_{k}\right) \log \left(1-\mathbf{z}_{k}\right)\right]$。

可以看到，DAE 有两个功能：一是对输入进行编码，即保留输入中的有关信息；二是尝试消除应用于输入的随机损坏过程的影响。其中，后者只能通过捕捉输入之间的统计依赖关系来完成。也就是说，DAE 试图从未损坏的值中预测随机损坏的值。注意到，能够从其余变量中预测任何变量子集是完全捕获一组变量之间的联合分布的充分条件，这也是 Gibbs 采样的工作原理 [5]。可以看出，这里提到的随机损坏过程与目前已经在训练神经网络时广泛使用的 Dropout 非常相似（然而，DAE 的提出时间要早于 Dropout）。

原论文同时通过流形学习、信息论、生成模型等多种角度对 DAE 进行解释。其中，从流形学习（manifold learning）视角来看，如下图所示，DAE 可以看作是一种学习一个流形的方式。假设训练数据（下图中标x 的数据）聚集在一个低维流形的周围，那么损坏数据（下图中标.的数据）通过损坏过程得到，它们距离流形较远。因此，整个模型试图将损坏数据投影回流形上，这样的模型更加稳健。而中间层表征可以被解释为流形上点所在的坐标系。

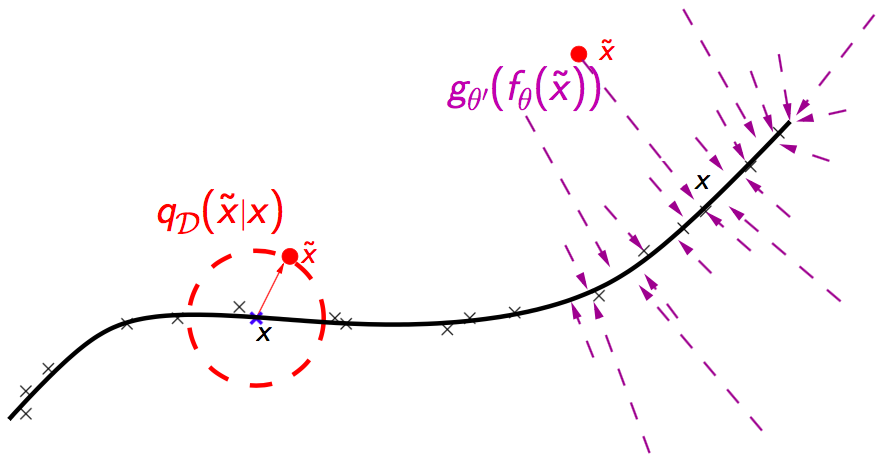
DAE-in-manifold-learning-perspective

收缩自动编码器

同样是为了抑制过拟合，收缩自动编码器（Contractive AutoEncoder, CAE）[6] 采用的方法是与正则化相结合，在损失函数中加入编码器的雅克比（Jacobian）矩阵范式来约束。

$$\mathcal{J}_{\mathrm{CAE}}(\theta)=\sum_{x \in D_{n}}\left(L(x, g(f(x)))+\lambda\left\|J_{f}(x)\right\|_{F}^{2}\right)$$

上式是 CAE 的损失函数，可以看到其分为两部分，第一部分是原始自动编码器的损失函数，用于最小化重构误差；而第二部分是 F 范式下的雅克比矩阵，如下：

$$\left\|J_{f}(x)\right\|_{F}^{2}=\sum_{i j}\left(\frac{\partial h_{j}(x)}{\partial x_{i}}\right)^{2}$$

想要最小化损失函数，就要使得偏导尽可能小，从而使模型对局部的抖动具有健壮性。这样，在第一部分保留最具代表性的特征信息的同时，第二部分倾向于丢掉所有特征信息，两者的共同作用即是只保留具有代表性的好的特征信息。

和 DAE 相比，CAE 主要挖掘样本内在的特征，使用样本本身的梯度信息，而不考虑样本中未出现的情况；而 DAE 对输入加入了噪声，改变了原数据的分布，因此对样本中未出现的测试数据同样具有健壮性。同时，DAE 的实现比 CAE 要简单，无需计算隐藏层的雅克比矩阵。

稀疏自动编码器

自动编码器除了可以学习低维表征外，也可以学习高维的稀疏表征。为了学习得到稀疏的表征，稀疏自动编码器（Sparse Autoencoder）在原来的损失函数中加入了一个控制稀疏化的正则项。最常见的思路是使用 L1 范数（对所有输出简单求和）来作为度量表征稀疏性的正则项，然而少有稀疏自动编码器的相关论文采用这种方法。

由于神经网络的稀疏性还可以被解释为单个神经元被激活的概率很小，因此我们先指定一个稀疏性参数 $\rho$ 来代表隐藏层神经元的平均激活程度，$\rho$ 是一个很小的值（例如 0.05）。这样，我们就可以引入一个度量来衡量神经元的实际激活度 $\hat \rho$ 与期望激活度 $\rho$ 之间的差异，然后将这个度量作为惩罚项即可。一般我们会选择 KL 散度（Kullback-Liebler Divergence）来作为度量，则有

$$\mathrm{KL}\left(\rho \| \hat{\rho}_{j}\right)=\rho \log \frac{\rho}{\hat{\rho}_{j}}+(1-\rho) \log \frac{1-\rho}{1-\hat{\rho}_{j}}$$

损失函数为

$$\mathcal{J}_{\mathrm{sparse}}(\theta)=\mathcal{J}_{\mathrm{AE}}(\theta)+\beta \sum_{j=1}^{n} \mathrm{KL}\left(\rho \| \hat{\rho}_{j}\right)$$

稀疏自动编码器的优点是有很高的可解释性，同时进行了隐式的特征选择。

LSTM 自动编码器 & 卷积自动编码器

在自动编码器的后续发展中，人们也开始想到，编码器和解码器不一定要表示为多层感知器。因此，自动编码器开始和各具特色的其他常用神经网络结构相结合，从而得到卷积自动编码器（Convolutional Autoencoder）、LSTM 自动编码器（LSTM Autoencoder）等模型。单纯的神经网络和与神经网络相结合的自动编码器的主要区别在于，单纯的神经网络通常用于监督学习的特定任务上，经过端到端的训练来学习内部的权重，提取的特征与任务紧密结合；而与神经网络相结合的自动编码器学习得到能够尽可能重建输入的结构权重，这样提取的特征可以应用于更多的任务。

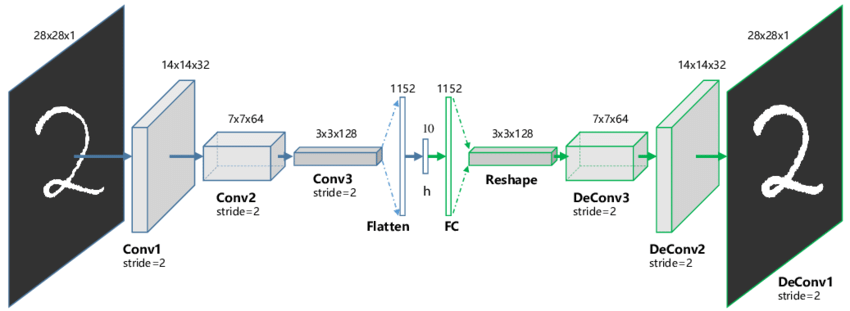
在计算机视觉的各种任务中，精心设计的卷积自动编码器已经成为各大模型不可或缺的部分。不管结构如何改变，其核心思想还是先通过多个卷积层（以及池化层）将高维图片降维得到向量表示，之后将反卷积网络（Deconvolution Network）组成解码器，来将特征向量重构为输入。想进一步了解反卷积可见 [8]。

本身适用于各类序列建模的 LSTM 在与自动编码器结合后，更是焕发了强大的活力。以学习句子的表征为例，在下图中，作为编码器的 LSTM 的每一步接受一个单词（的 embedding）和上一步的隐藏状态作为输入。当最后一个单词被输入时，对应的神经元的隐藏状态作为表征，输入到作为解码器的 LSTM 中。在解码器中，每一个单元将上一步的隐藏状态和输出（也可以是输出对应的标签）作为输入，通过 softmax 层预测对应的词并输出，从而重构出输入的句子。

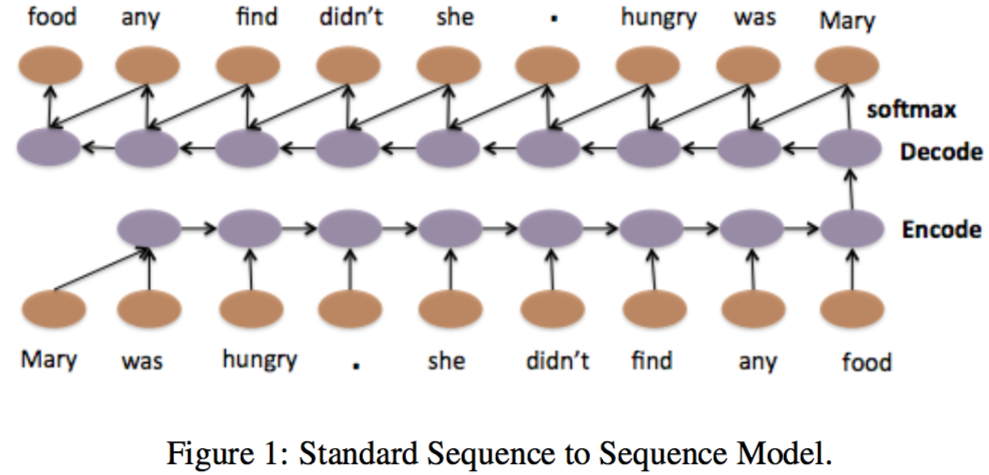
实际上，对于 NLP 略有所知的同学们应该早已看出，将输出目标从原始输入换成监督学习任务中的有标注数据，LSTM 自动编码器有一个更为响亮的名字：Seq2Seq（Sequence to Sequence）。Seq2Seq 结构存在两个问题，一是将整个句子的信息压缩为一个低维向量，会造成信息损失；二是句子如果过长，长程依赖很难被完全学习，从而使得准确率下降。因此，人们把 Seq2Seq 结构与注意力机制（Attention Mechanism）相结合，由此推动了 NLP 领域的蓬勃发展。当然，这与本篇博客的主要内容已相去甚远，因而不再详述。

可以看出，将常用神经网络结构与自动编码器相结合其实更多是一个大概的思想，在具体实现时，编码器和解码器可以自由变换，例如 LSTM 自动编码器中可以将 LSTM 换成 GRU，或者将单向 LSTM 换为双向。总而言之，两者的结合使得双方都获得了新的可能性。

参考资料

引用

扩展