自动编码器一览(二)
这是“自动编码器一览”系列的第二篇博文。在本文中,我会介绍一些最近看过并且比较感兴趣的自动编码器的变形,说是介绍,可能更像是论文笔记合集。比起第一篇提到过那些更为通用的经典变形,这些相对而言比较新颖的自动编码器在结构上进行修改,使得它们更符合所对应的特定任务的需求。如果我之后又看到一些有意思的自动编码器,也可能在这篇博文中继续更新。
本文中包含以下内容:
- 递归自动编码器(Recursive Autoencoder)
- Additional Stacked Denoising Autoencoder(aSDAE)
“自动编码器一览”系列:
递归自动编码器
我们首先介绍论文 “Semi-Supervised Recursive Autoencoders for Predicting Sentiment Distributions”[1] 提出的递归自动编码器(Recursive Autoencoder)。在这篇论文中,递归自动编码器被用于通过无监督或半监督的训练方式,学习不定长句子的表征向量。这样学习到的表征可以被用于下游任务。在情感预测任务上,递归自动编码器达到了当时的 state-of-the-art。递归自动编码器最大的创新之处是加入了独特的层次结构,并使用语义的组合来理解情感。递归自动编码器既可以在没有标签的领域数据上,也可以在有标签的情感数据上进行训练。
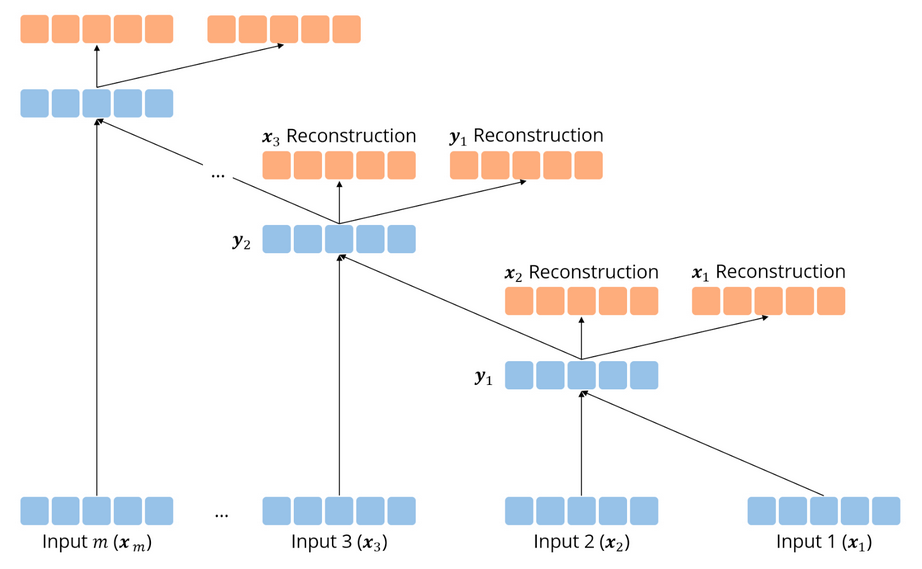
传统递归自动编码器
传统递归自动编码器要求在以一组词向量的形式给出要输入的句子 $(x_1, x_2, \dots, x_m)$ 的同时,给出句子的二叉树形结构,这个树形结构通过一组父节点和两个子节点的三元组表示:$(p \rightarrow c_{1} c_{2})$。例如在图中,我们有 $((y_{1} \rightarrow x_{1} x_{2}), (y_{2} \rightarrow y_{1} x_{3}), \dots)$ 等三元组。因为对于每组子节点,我们使用同一个神经网络来处理,因此 $y_i$ 的维度和 $x_i$ 相同。
对于每个三元组 $(p \rightarrow c_{1} c_{2})$,我们通过公示:
$$p=f\left(W^{(1)}\left[c_{1} ; c_{2}\right]+b^{(1)}\right),$$
来得到父节点 $p$ 的表征。注意 $f(\cdot)$ 表示非线性的激活函数。为了评估父节点 $p$ 的表征有多好,我们从父节点的表征重建其两个子节点的表征(图中橙色的节点):
$$\left[c_{1}^{\prime} ; c_{2}^{\prime}\right]=W^{(2)} p+b^{(2)}$$
在训练过程中,我们的目标就是最小化这个重建的误差。对于每个子节点对,我们使用欧式距离来计算误差:
$$E_{r e c}\left(\left[c_{1} ; c_{2}\right]\right)=\frac{1}{2}\left|\left[c_{1} ; c_{2}\right]-\left[c_{1}^{\prime} ; c_{2}^{\prime}\right]\right|^{2}$$
我们只需要自底向上来重复以上步骤即可。
用于预测结构的无监督递归自动编码器
我们可以从三个方面来优化传统的递归自动编码器。
第一点是,对于输入的句子 $x$,不再需要给出其树形结构,而是自己构建。方法是使用贪婪算法在每一步去尝试每个可能选择的子节点,最后选择这一步重构损失最低的方式构建整棵树。
第二点是,之前采用的重构损失是平均的惩罚所有父节点的子节点重构损失。一个改进是,对于更上层的、包含更多单词的子节点对应的重构损失,给一个更高的权重,因为它对这个句子的表征的影响更大。例如,在重构时,设 $n_1$ 和 $n_2$ 是潜在子节点 $c_1$ 和 $c_2$ 包含的单词数量,则重新定义重构损失为
$$E_{r e c}\left(\left[c_{1} ; c_{2}\right] ; \theta\right)= \frac{n_{1}}{n_{1}+n_{2}}\left|c_{1}-c_{1}^{\prime}\right|^{2}+\frac{n_{2}}{n_{1}+n_{2}}| | c_{2}-c_{2}^{\prime}| |^{2}$$
第三点是,由于每次得到的父节点表征会马上被用于重建,因此为了降低重构误差,机器会倾向于学习值非常小的表征。为了避免这个现象出现,在每次计算得到父节点的表征 $p$ 时,可以做一个正则化 $p = \frac{p}{| p |}$。
半监督递归自动编码器
到现在为止,递归自动编码器已经可以无监督地生成捕捉了句子的语义结构的表征。我们将这个表征输入到下游任务的模型中,这样,可以通过下游任务的训练来进行微调,从而使模型学习在表征中包含更多对下游任务更为重要的信息。
Additional Stacked Denoising Autoencoder
接下来我们来到推荐系统领域,介绍在论文 “A Hybrid Collaborative Filtering Model with Deep Structure for Recommender Systems”[2] 被提出的 Additional Stacked Denoising Autoencoder(aSDAE)。如果一定要翻译的话,这个模型应该称为“有附加信息的堆叠去噪自动编码器”,因为这个名字有点太长了,因此我们在接下来的叙述中用 aSDAE 来代指这个自动编码器。
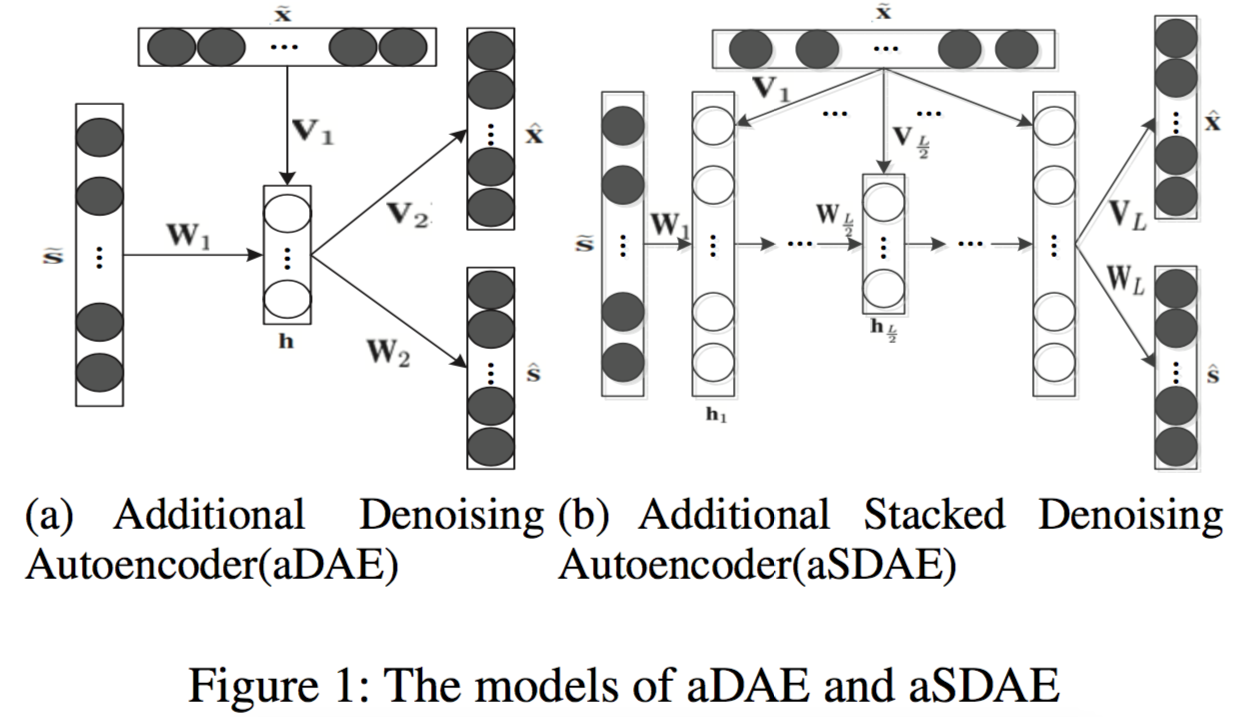
其实 aSDAE 的思想非常简单,就是在堆叠去噪自动编码器的基础上,受到 Seq2Seq 模型的启发,在每一层接受一个相同的、对应输入的附加信息(side information),然后在自动编码器的最后同时重构输入和附加信息。
用公式表示 aSDAE 模型。对于 aSDAE 的隐藏层 $l \in { 1, \dots, L-1 }$,其隐藏表征 $h_l$ 的计算方法为
$$h_{l}=g\left(W_{l} h_{l-1}+V_{l} \tilde{x}+b_{l}\right),$$
其中,$h_0 = \tilde{s}$ 是用噪声处理过的输入,$\tilde{x}$ 是附加信息,$f(\cdot)$ 和 $g(\cdot)$ 都是激活函数。
对于 aSDAE 的输出层 $L$,输出的计算为
$$\begin{aligned} \hat &=f\left({W}_{L} {h}_{L}+{b}_{\hat{s}}\right) \\ \hat &=f\left({V}_{L} {h}_{L}+{b}_{\hat{x}}\right) \end{aligned}$$
因此,aSDAE 的损失函数为
$$L = \alpha|{s}-\hat|_{F}^{2}+(1-\alpha)|{x}-\hat|_{F}^{2} + \lambda\left(\sum_{l}\left|{W}_{l}\right|_{F}^{2}+\left|{V}_{l}\right|_{F}^{2}\right),$$
其中,$\alpha$ 是一个用于保持平衡的超参数,$\lambda$ 是正则化参数。
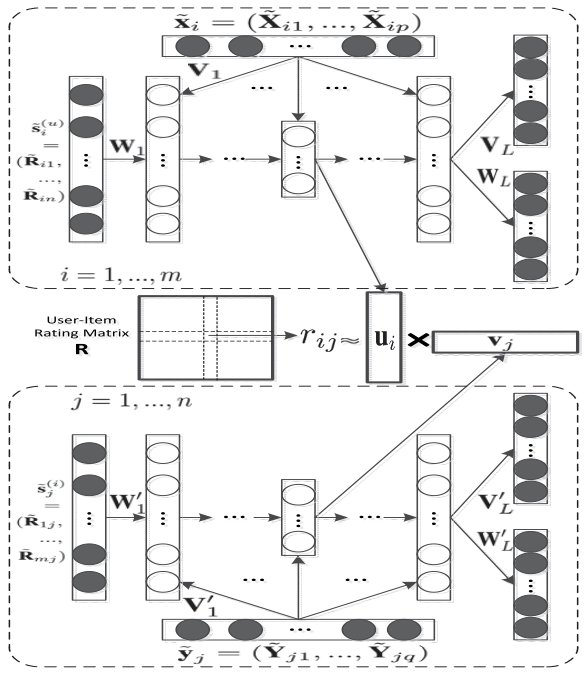
aSDAE 本身就介绍完了。在论文 [2] 中,aSDAE 学习用户和商品对应的隐向量矩阵,并将用户的基本个人信息、用户画像信息、物品的基本信息等附加信息引入,从而解决协同过滤中的稀疏性与冷启动问题。这些和推荐系统相关的背景知识就不多讨论了,有兴趣的同学可以看参考资料 [3]。
More Autoencoder
随着对自动编码器的深入了解,我们有两个问题可以讨论:
- 为什么要最小化重构误差?有没有其他做法?
- 怎么让自动编码器学习到的表征更具可解释性?
从这两个问题引入,李宏毅老师在他的机器学习课程上又对自动编码器的一些最新进展进行了介绍和讨论。有兴趣了解的同学可以查看我的《李宏毅机器学习》课程笔记:More Autoencoder - 《李宏毅机器学习》课程笔记,在此就不再重复写作了。而在“自动编码器一览”系列的下一篇中,我们会来看看可能是近年来的顶会上出现最多的自动编码器的一种形式——变分自动编码器。
参考资料
- [1] Richard Socher, Jeffrey Pennington, Eric H.Huang, Andrew Y.Ng, Christopher D.Manning. “Semi-Supervised Recursive Autoencoders for Predicting Sentiment Distributions”, EMNLP 2011
- [2] Xin Dong, Lei Yu, Zhonghuo Wu, Yuxia Sun, Lingfeng Yuan, Fangxi Zhang. “A Hybrid Collaborative Filtering Model with Deep Structure for Recommender Systems”, AAAI 2017
- [3] 推荐系统中基于深度学习的混合协同过滤模型. https://zhuanlan.zhihu.com/p/25234865