【paper reading】2021 小样本分割论文选读

根据手头想法的需要，读一读 2021 年顶会顶刊的小样本分割相关论文并做笔记于此。有开源代码的论文优先，持续更新。

• Prior Guided Feature Enrichment Network for Few-Shot Segmentation (TPAMI 2020)
• Few-Shot Segmentation Via Cycle-Consistent Transformer (NeurIPS 2021)
• Simpler is Better: Few-shot Semantic Segmentation with Classifier Weight Transformer (ICCV 2021)
• Few-Shot Segmentation Without Meta-Learning: A Good Transductive Inference Is All You Need? (CVPR 2021)
• Self-Guided and Cross-Guided Learning for Few-Shot Segmentation (CVPR 2021)
• Adaptive Prototype Learning and Allocation for Few-Shot Segmentation (CVPR 2021)
• Mining Latent Classes for Few-shot Segmentation (ICCV 2021)
• Few-Shot 3D Point Cloud Semantic Segmentation (CVPR 2021)

Prior Guided Feature Enrichment Network for Few-Shot Segmentation

TPAMI 2020 | arxiv | github

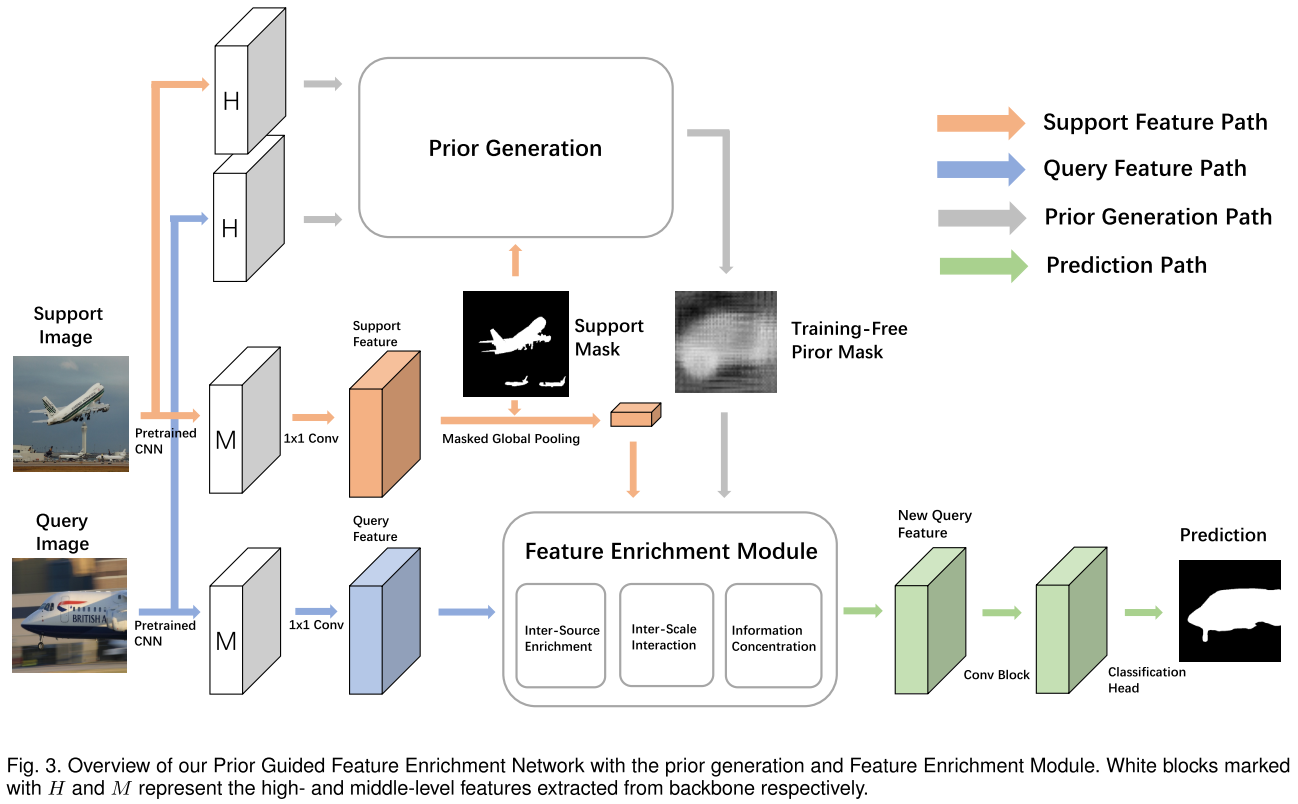
这篇工作被很多 2021 年的相关论文作为 baseline 并且效果仍然有竞争力，因此先介绍一下。该论文提出了 Prior Guided Feature Enrichment Network (PFENet) 来解决两个问题：(1) 很多分割方法都依赖于 high-level 特征，然而 CANet, CVPR 2019 的实验结果表明小样本模型仅仅使用 high-level 特征会导致表现下降；(2) 样本数量过少会导致 support 物体的尺寸和姿态都和 query target 有很大不同，在该文中被称为 spatial inconsistency，并且 ablation study 的实验结果表明仅仅集成 multi-scale 结构对于该问题只是次优解。因此，本文提出了以下两点贡献：

prior generation：使用 high-level 特征（实践中是 conv5_x 的最后一层的输出）来生成 prior mask。在用 support mask 遮盖提取的 support 特征后，计算 support 和 query 特征的 pixel-wise cosine 相似度。对于 query 中的每个像素，取其和所有 support 像素的相似度中的最大值来得到 prior mask。之后 prior mask 经过 min-max normalization 来将所有值放缩到 [0, 1] 范围。如果 shot 数大于 1，将同一 query 特征和不同 support 特征得到的多张 prior masks 求平均来得到最终的 prior mask 输入到 FEM。

Feature Enrichment Module (FEM)：这一块看下图比较好理解，就是用多个 average pooling 来将 query 特征、support prototype 和 prior mask 的拼接产物放缩到不同大小，然后做 multi-scale 的信息交互。注意 query 特征和 support 特征是通过拼接 middle-level 特征（实践中是 conv3_x、conv_4x 的最后一层的输出）得到，另外如果 shot 数大于 1，直接取所有处理后的 support 特征的均值作为新的 support 特征。inter-scale interaction 的每个 scale 的产物也会过一个 3x3 + 1x1 的卷积层组成的分类头得到损失 $\mathcal{L}^i_1$，然后所有 scale 产物拼接后经过 1x1 卷积也用分类头得到损失 $\mathcal{L}_{2}$。最终的总损失为 $\mathcal{L} = \frac{\sigma}{n}\sum^n_{i=1} \mathcal{L}^i_1 + \mathcal{L}_{2}$，$\sigma$ 在所有实验中设为 1.0。

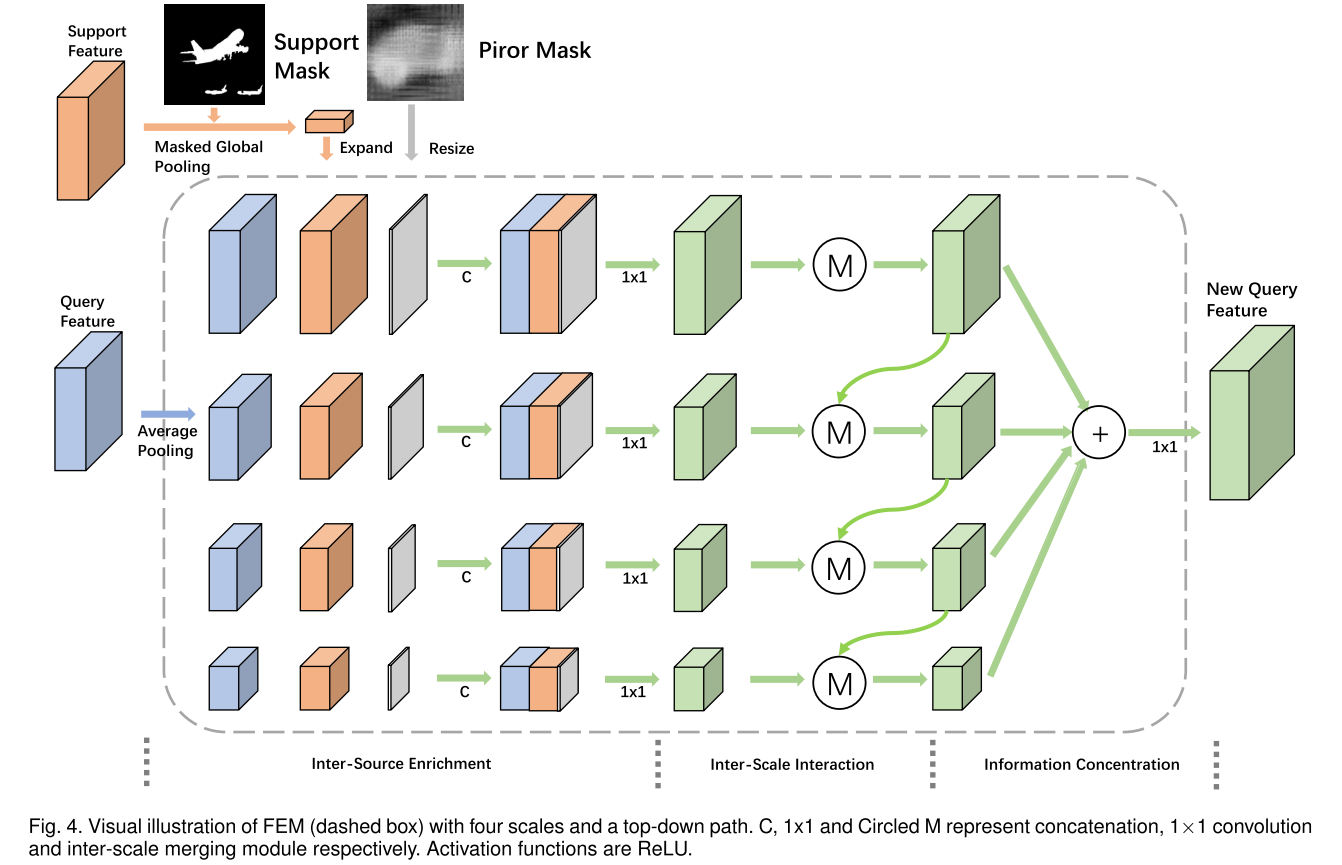
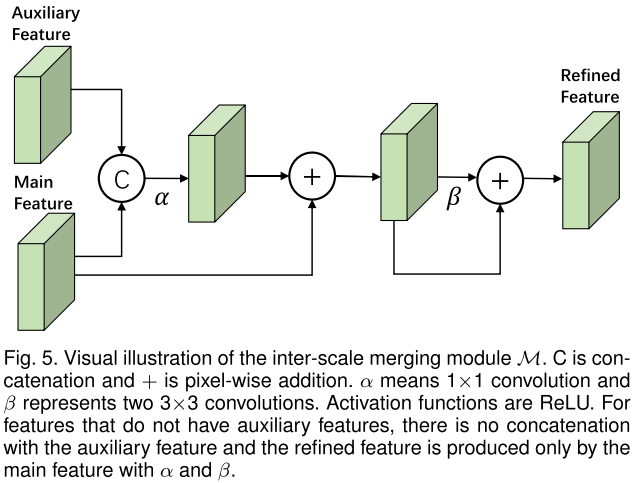
一个稍微需要注意的点是图中带圈的 M 的结构如下图所示，其中 auxiliary 特征指 finer 特征，main 特征指 coarse 特征。对于没有 auxiliary 特征的 main 特征（如上图最上面的一个 scale），省略下图的第一步拼接操作。

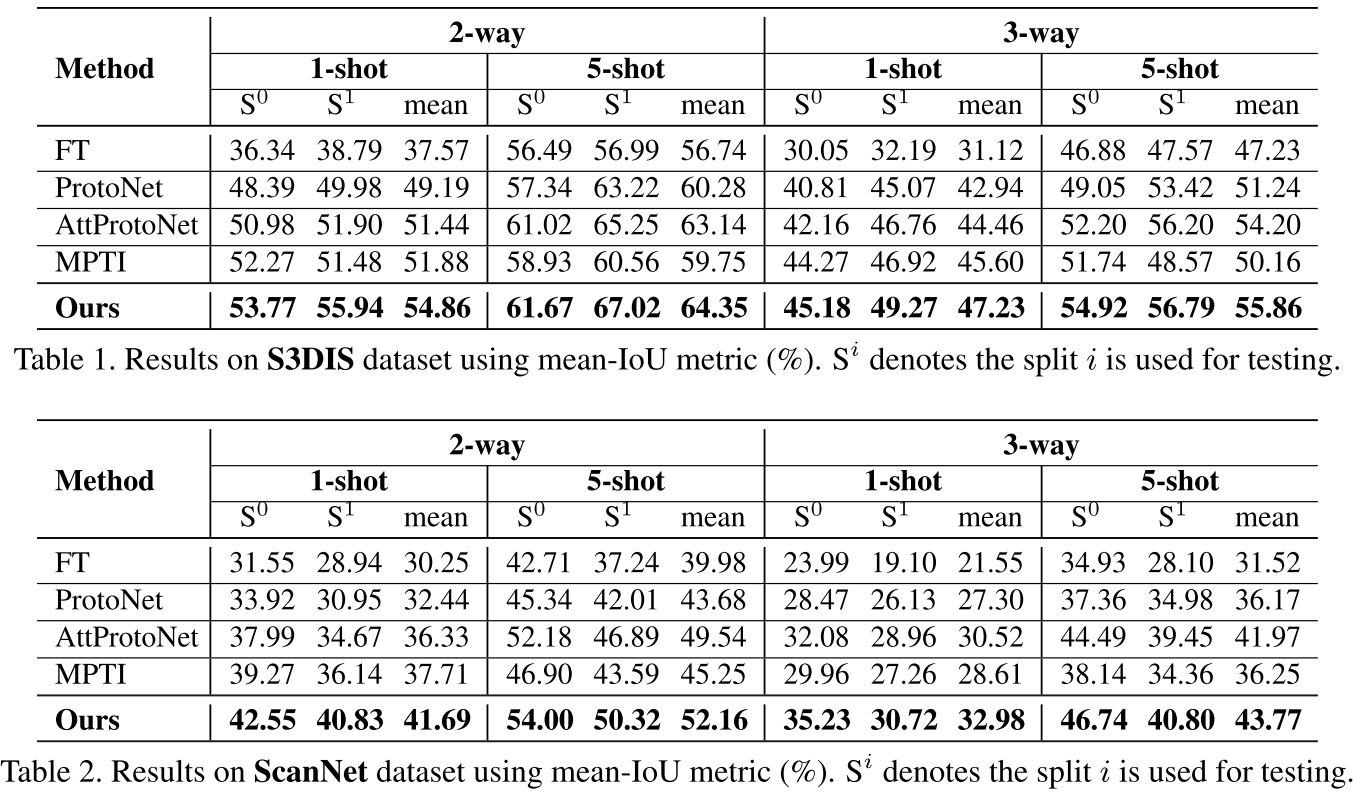
实验结果：

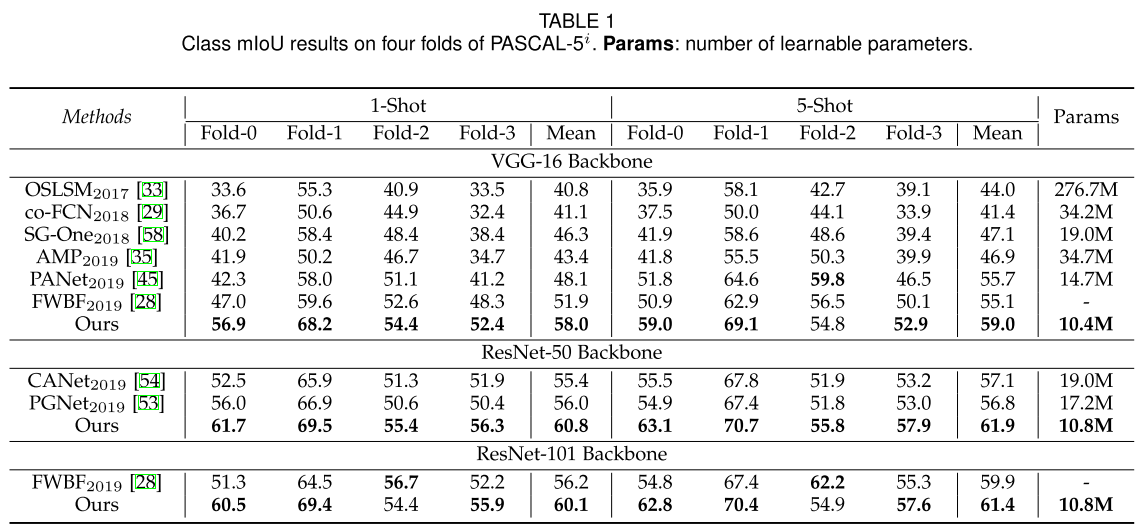
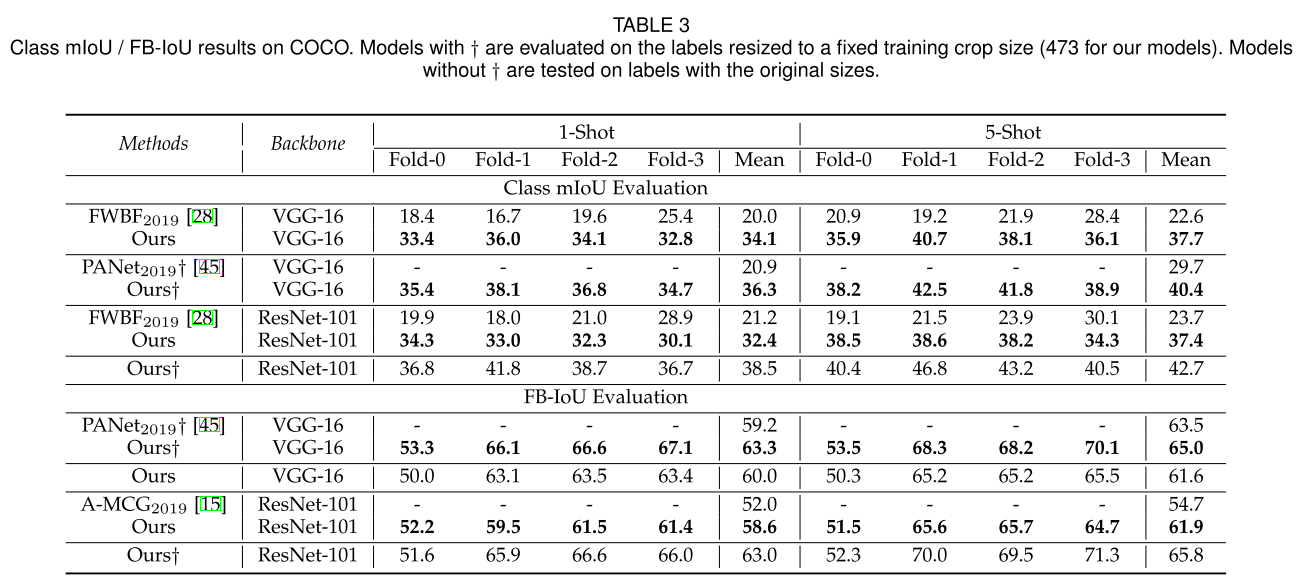
Few-Shot Segmentation Via Cycle-Consistent Transformer

NeurIPS 2021 | link | github（尚未包含代码）

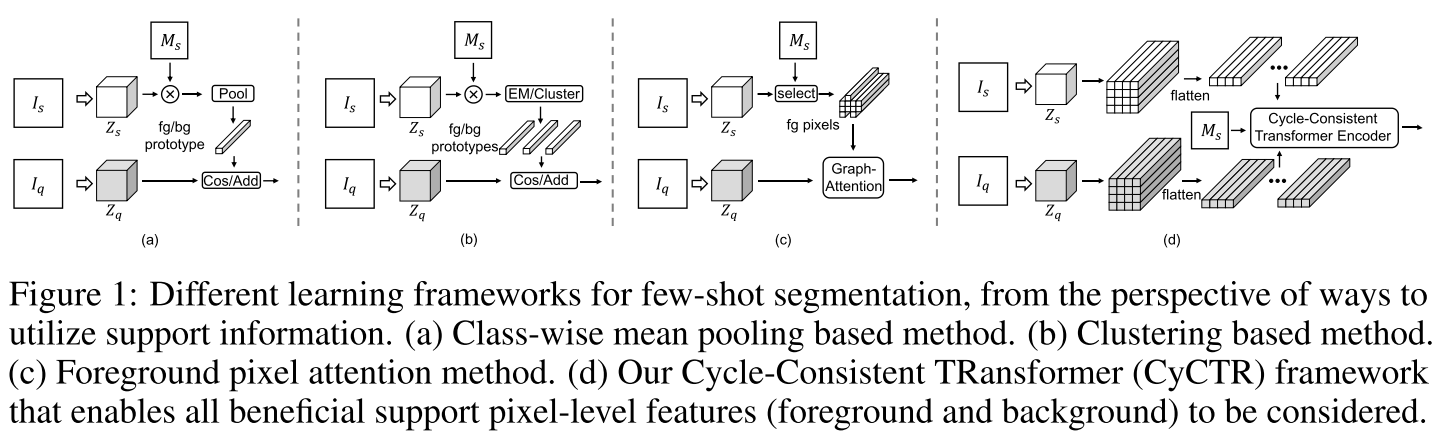
已有的小样本分割工作通常从 support 的图像特征提取 semantic-level prototypes，其中根据可以分为两类：(1) 如上图 (a) 所示的 class-wise mean pooling (PANet, ICCV 2019; SG-One, IEEE Trans. Cybern., 2020; CANet, CVPR 2019)，将属于不同类别的区域的特征算均值得到 prototypes；(2) 如上图 (b) 所示的 clustering，使用 EM 算法 (RPMM, ECCV 2020) 或者 K-means (PPNet, ECCV 2020) 来生成多个 prototypes 。然而，基于 prototypes 的方法会导致不同程度的 support information 的损失。因此，一些工作 (PGNet, ICCV 2019; DAN, ECCV 2020) 用 attention 机制来从 support 前景像素提取信息。然而，这些方法忽略了存在对分割有帮助的信息的 support 背景像素；同时，support 和 query 图像间的包含尺度、颜色、场景等差别使得只有一小部分 support 像素是对 query 图像的分割有帮助，而另一些 support 像素会和 query 的前景像素有很大差别，导致 attention 无法准确表示语义上的对齐。

本文提出了 Cycle-Consistent Transformer (CyCTR) 模块，包含两种 Transformer 部件：(1) self-alignment block：通过聚合相关的上下文信息来编码 query 的图像特征，Query、Key 和 Value 都来自同个 embedding；(2) cross-alignment block：将 support 图像的 pixel-wise 特征聚合到 query 图像的 pixel-wise 特征中，query 图像的特征是 Query，support 图像的特征作为 Key 和 Value。另外，一种新的 cycle-consistent attention 被部署在 cross-alignment block 上。从一个 support 像素的特征出发，我们找到它在 query 特征上的最近邻，然后在找到与这个最近邻最相似的 support 特征。如果起点和终点的 support 特征属于同一类别，就称作建立起了 cycle-consistency relationship。这个操作被集成到 attention 中来让 query 特征只去注意 cycle-consistent support 特征。因此，我们可以在避免将 bias 引入到 query 特征的前提下，利用 support 的背景像素。

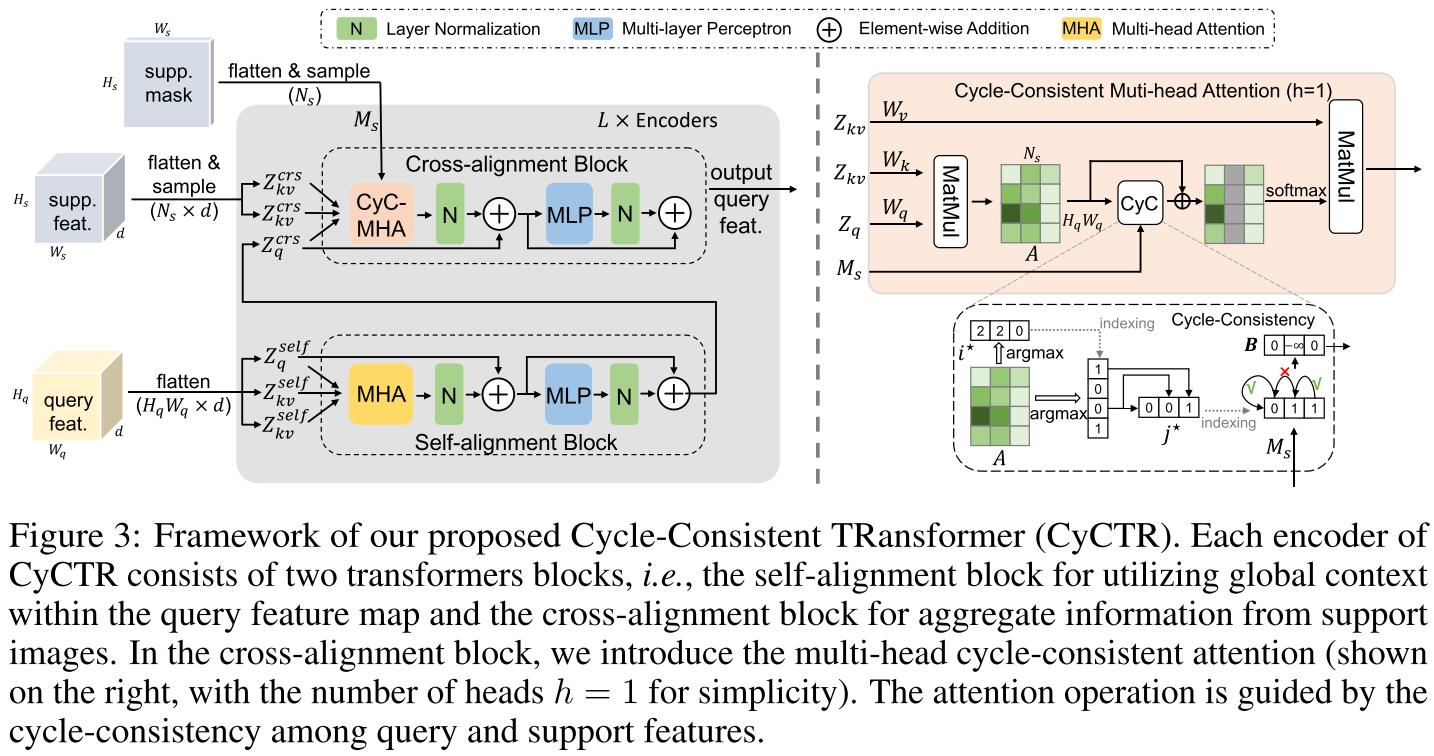
具体实现上，support 和 query 特征都被拉伸成 1D 序列输入到 transformer 中，序列的长度分别为 $H_qW_q$ 和 $N_s$。如上图所示，$L$ 个编码器堆叠起来，每个编码器输出的 query 特征被输入到下一个编码器中的 self-alignment block，直到最终输出的 query 特征进行 pixel-wise 的分类。在 cross-alignment block 中，首先计算一个 affinity map $A = \frac{QK^T}{\sqrt{d}}, A \in \mathbb{R}^{H_qW_q \times N_s}$ 来度量所有 query 和 support 像素的关联度。然后，对于第 $j$ 个 support 像素，可以找到与其最相似的 query 像素 $i^{\star}=\text{argmax}_i A_(i,j)$。然后再返回找到与 query 像素 $i^{\star}$ 最相似的 support 像素 $j^{\star}=\text{argmax}_j A_(i^{\star},j)$。给定 support 像素标签 $M_s \in \mathbb{R}^{N_s}$，获得一个 additive bias $B \in \mathbb{R}^{N_s}$：

$$B_{j}= \begin{cases}0, & \text { if } M_{s(j)}=M_{s\left(j^{\star}\right)} \\
-\infty, & \text { if } M_{s(j)} \neq M_{s\left(j^{\star}\right)} \end{cases}$$

则对于位置为 $i$ 的单个 query token（即像素）$Z_{q(i)} \in \mathbb{R}^d$，通过下式来聚合 support 信息：

$$\text{CyCAtten}(Q_i, K_i, V_i) = \text{softmax}(A_{i} + B)V$$

当在 self-alignment block 中执行 self-attention 时，也可能存在 query token 聚合到无关甚至是有害的特征（尤其当背景较为复杂时）。然而，由于没有 query 像素的标签，无法在 query 的像素上执行 cycle-consistent attention。受到 DeformableAttention (ICLR 2021)，可以通过学习的方式获得 consistent 像素 $\triangle = f(Q + \text{Coord}), \triangle \in \mathbb{R}^{H_pW_p \times P}$ 以及对应的 attention weights $A^{} = g(Q + \text{Coord}), A^{} \in \mathbb{R}^{H_qW_q \times P}$，$P$ 代表被聚合的像素的数量。$\text{Coord} \in \mathbb{R}^{H_qW_q \times N_s}$ 是位置编码，$f(\cdot)$ 和 $g(\cdot)$ 是用于预测 offsets 和 attention weights 的全连接层。因此，self-alignment block 中的 self-attention 可以被表示为：

$$\text{PredAtten}(Q_r, V_r) = \sum^P_g\text{softmax}(A^{`})_{(r,g)}V_{r+\triangle_{r,g}}$$

其中，$r \in {0,1, \dots, H_qW_q}$ 是拉伸的 query 特征的 index，$Q$ 和 $V$ 通过对拉伸的 query 特征用可学习的参数进行线性变换得到。

以上讨论的是 1-shot 的情况。当 shot 数大于 1 时，可以将所有 support 特征拉伸并拼接作为输入。然而这样会导致计算量过大，因此可以采取一个非常简单的 mask-guided sampling 策略来减小计算复杂度。给定 $k$-shot support 特征 $Z_s \in \mathbb{R}^{kH_sW_s \times d}$，support tokens（即像素）通过从所有 support 图像的前景区域均匀随机采样 $N_{fg}$ 个（$N_{fg} \leq \frac{N_s}{2}$，其中 $N_s \leq kH_sW_s$）和从背景区域采样 $N_s - N_{fg}$ 个得到。通过选择一个合适的 $N_s$，这个策略既能有效减少计算量，也能够帮助平衡前景和后景的比例。

方法的整体框架如下图所示。值得注意的是，该方法还是先用 PFENet (TPAMI 2020) 对 support 和 query 的特征进行了处理再输入到 cycle-consistent transformer 中。

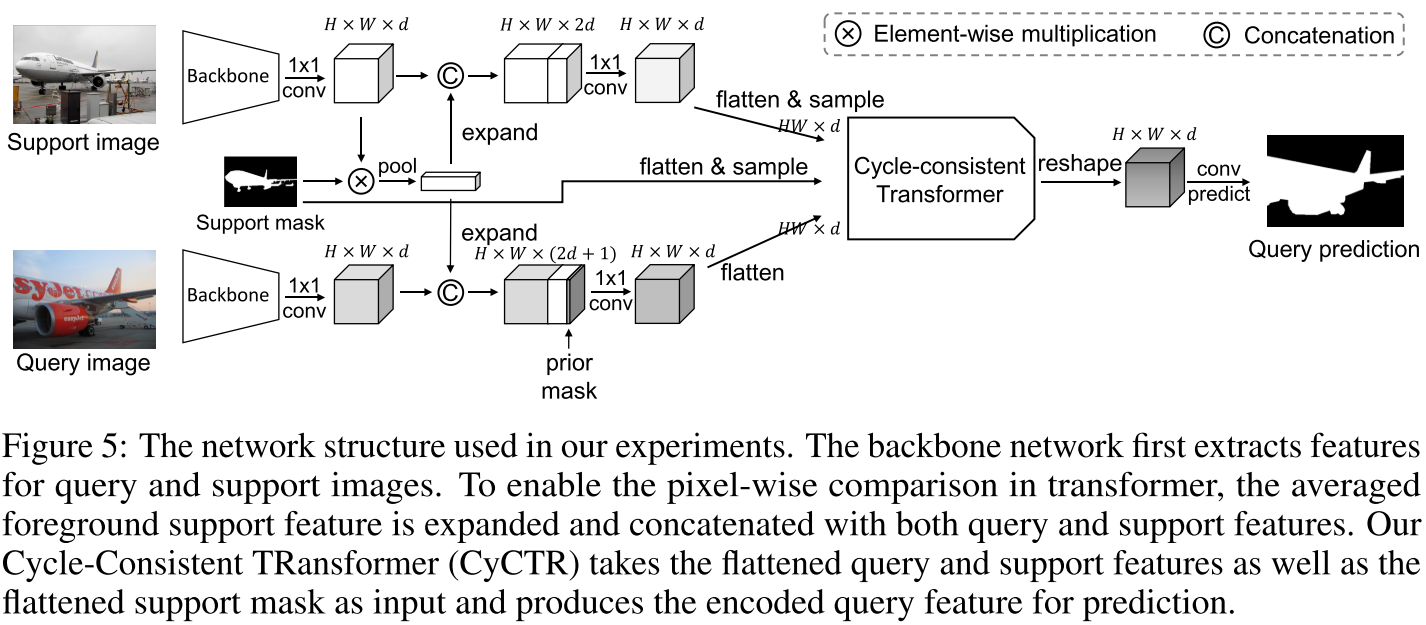
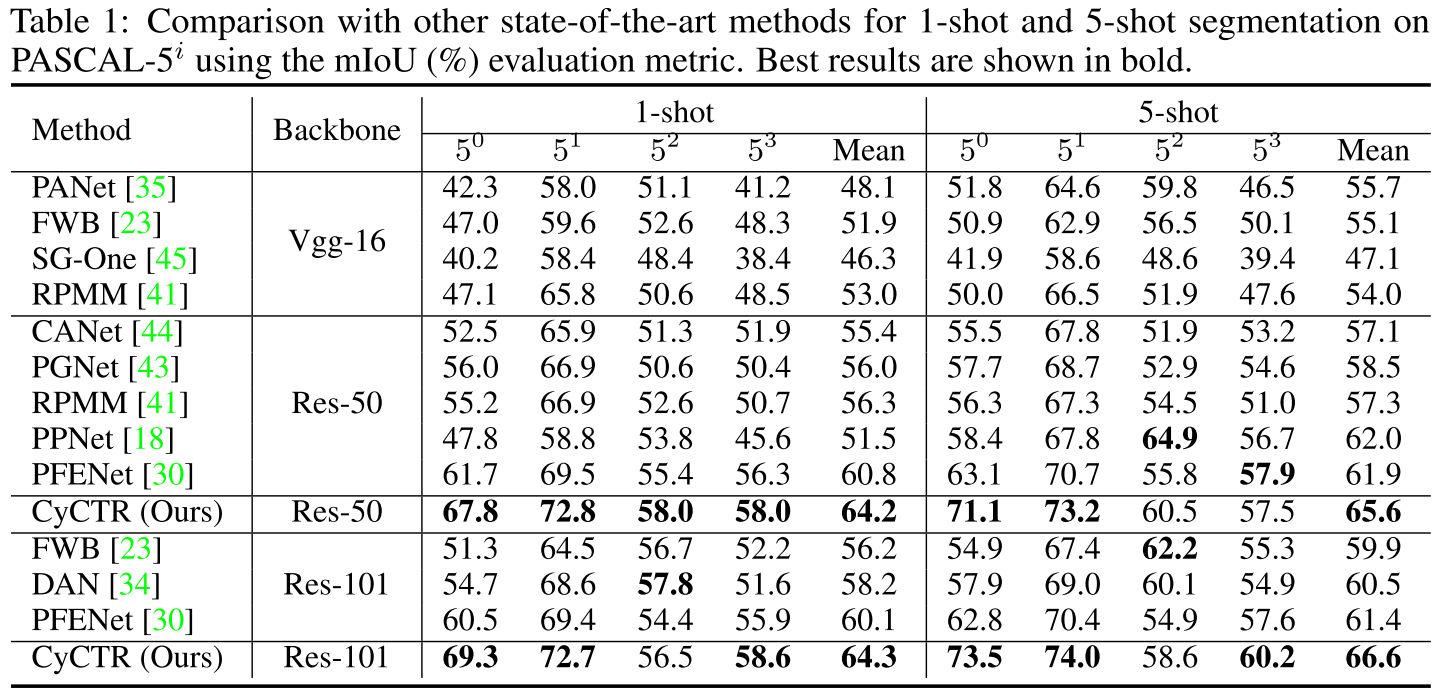
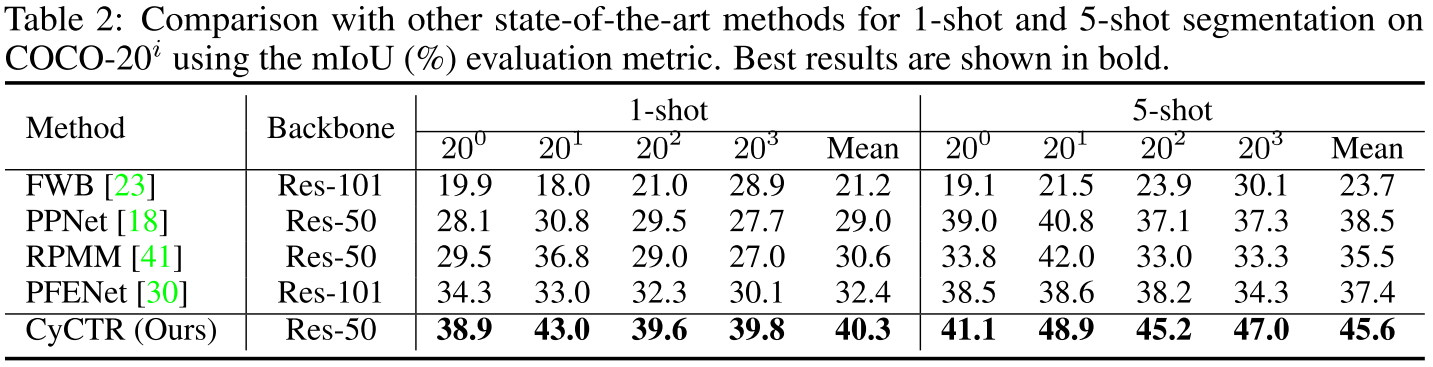
实验结果：

Simpler is Better: Few-shot Semantic Segmentation with Classifier Weight Transformer

ICCV 2021 | arxiv | github

分割模型通常由编码器、解码器和一个简单的分类器（通常是一个 1x1 卷积层，参数 $\mathbf{w} \in \mathbb{R}^{2 \times d}$ 用于将 $d$ 个 channel 映射来二分类以区分前景和背景像素）组成。现有的一些小样本分割方法对三部分的参数都进行元学习。而本文提出考虑到样本量极少，三部分的参数都快速适应到新类仍然很难。因此，本文提出元学习阶段只关注分类器，而采用预训练的方式来处理编码器和解码器（本文采用 PSPNet (CVPR 2017) 作为骨干分割网络），认为在经过大量基类的数据训练后它们能够泛化到新类上。之后，编、解码器的参数被冻结。在元学习阶段，首先使用 support 样本来训练分类器参数 $\mathbf{w}$。本文提出这样得到的总体模型的表现已经能够超越（当时的）SOTA PPNet (ECCV 2020)，如下表 1、5 所示：

然而，本文继续提出，由于较大的类内变化（或者说类内差异）的存在，在 support 样本上学到的 $\mathbf{w}$ 无法很好地适应到每个 query 样本上。因此，本文提出 Classifier Weight Transformer (CWT)，在元学习阶段去学习每个 query 样本特定的分类器权重。模型流程图如下图所示：

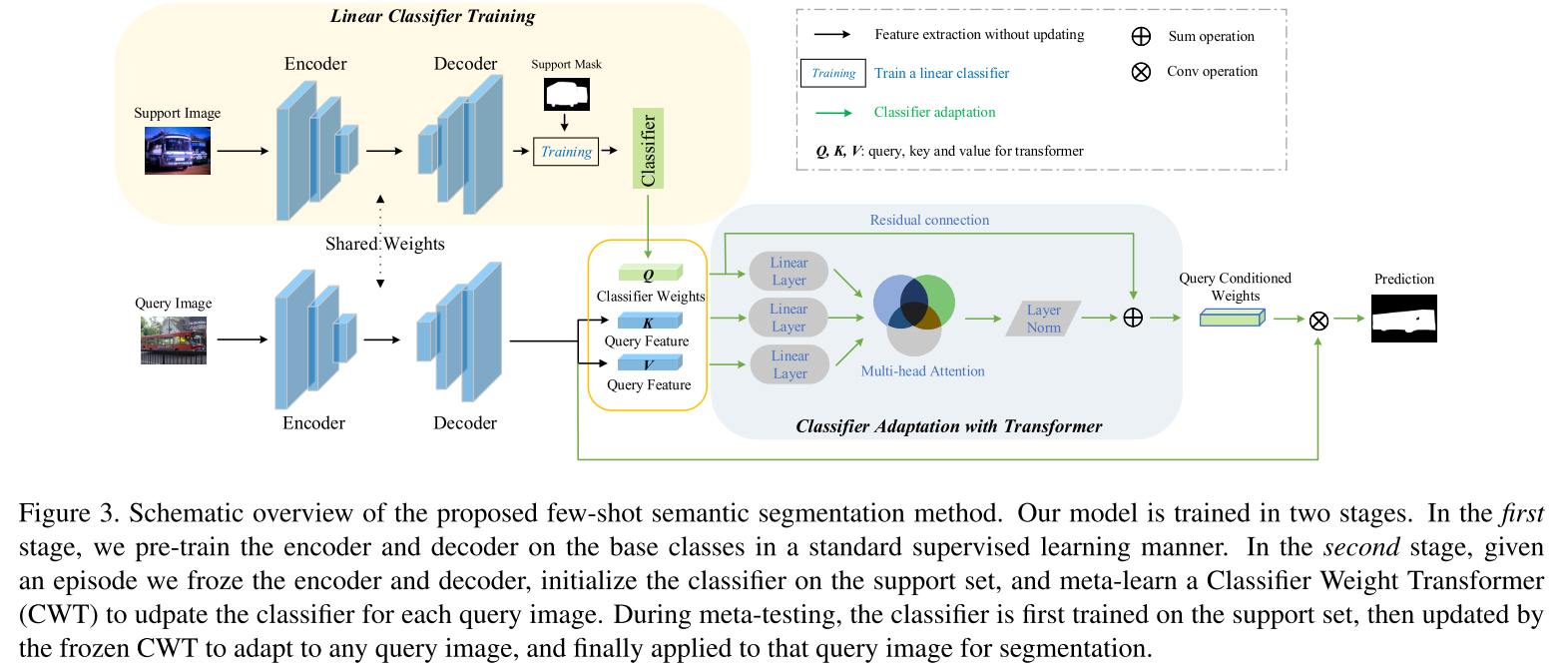
具体地，CWT 中的 self-attention 可以被表示为：

$$\mathbf{w}^{*}=\mathbf{w}+\psi\left(\text{softmax}\left(\frac{\boldsymbol{w} \mathbf{W}_{q}\left(\boldsymbol{F} \mathbf{W}_{k}\right)^{\top}}{\sqrt{d_{a}}}\right)\left(\boldsymbol{F} \mathbf{W}_{v}\right)\right)$$

其中，$\boldsymbol{F} \in \mathbb{R}^{n \times d}$ 代表 query 样本 $n$ 个像素提取出的特征，$\mathbf{W}_{q}/\mathbf{W}_{k}/\mathbf{W}_{v} \in \mathbb{R}^{n \times d_{a}}$ 是可训练参数，而 $\mathbf{w}^{*}$ 即是将用在该 query 样本上的参数。CWT 的直觉是，相比背景像素，通常情况下 query 中的前景像素特征会和 $\mathbf{w}$ 计算得到更大的相似度，因此可以据此调整 $\mathbf{w}$。在（元）测试阶段，CWT 的参数也是冻结的。

除开表 1、5 外的其他实验结果：

Few-Shot Segmentation Without Meta-Learning: A Good Transductive Inference Is All You Need?

CVPR 2021 | link | github

本文提出现有的小样本分割工作所遵循的两个假设在现实场景中通常是不可用的：(1) episodic training 假设 testing tasks 的 support shots 数量和 meta-training 阶段使用的任务保持一致；(2) base 和 novel 类别通常被假设从同一数据集中采样得到。针对假设 (1)，本文的思想与 Transductive Fine-Tuning, ICLR 2020 等小样本识别方法有共通之处，提出精心设计的 transductive fine-tuning 的方法 RePRI (Region Proportion Regularized Inference)，能够用线性的分类器取得 SOTA。针对假设 (2)，本文也引入了 cross-domain 的设置，即 base 和 novel 类别来自不同的数据集，并在 COCO->PASCAL 上取得 SOTA。

在 meta-training 阶段，RePRI 不采用 episodic training，而是用整个 base set 和标准交叉熵来训练特征提取器。在每个 testing task 进行 inference 时，RePRI 在优化时采用的损失包含三项：

1. $\mathrm{CE}=-\frac{1}{K|\Psi|} \sum_{k=1}^{K} \sum_{j \in \Psi} \widetilde{y}_{k}(j)^{\top} \log \left(p_{k}(j)\right)$：标准的交叉熵 (cross-entropy, CE)，作用于 support 图像的有标签像素上。注意只使用这一项来进行优化通常导致过拟合于 support set，尤其是 1-shot 设置时；
2. $\mathcal{H}=-\frac{1}{|\Psi|} \sum_{j \in \Psi} p_{\mathcal{Q}}(j)^{\top} \log \left(p_{\mathcal{Q}}(j)\right)$：香农熵 (Shannon entropy)，作用于 query 图像像素的预测上，来使模型对 query 图像的预测更加有信心。直观来说，这一项让线性分类器的决策边界推向 query 特征空间的低密度区域。在对最初置信度较低的区域的预测有帮助的同时，仅仅将这项加入到损失中并不能解决 CE 导致的问题，甚至可能使表现进一步恶化，如下图 Figure 1 所示；
3. $\mathcal{D}_{\mathrm{KL}}=\widehat{p}_{\mathcal{Q}}^{\top} \log \left(\frac{\widehat{p}_{\mathcal{Q}}}{\pi}\right), \widehat{p}_{\mathcal{Q}}=\frac{1}{|\Psi|} \sum_{j \in \Psi} p_{\mathcal{Q}}(j)$：KL 散度，鼓励模型预测的背景/前景 (B/F) 比例接近于一个参数 $\pi \in [0, 1]^2$。论文指出这一项在损失中占关键位置，首先当参数 $\pi$ 与 query 图像的精确 B/F 比例不匹配时，该项有助于避免因 $\mathrm{CE}$ 和 $\mathcal{H}$ 最小化而导致的退化解；而如果能够准确估计 query 图像中的 B/F 比例（即有这个先验知识可供使用时），该项可以大幅提高方法整体的性能。

分类器的选择：RePRI 的线性分类器和 Baseline++, ICLR 2019 相似：$s^{(t)}(j)=\text{sigmoid}\left(\tau\left[\cos \left(z(j), w^{(t)}\right)-b^{(t)}\right]\right)$。其中原型 $w^{(0)}$ 是 support 前景特征的均值：$w^{(0)}=\frac{1}{K|\Psi|} \sum_{k=1}^{K} \sum_{j \in \Psi} \widetilde{y}_{k}(j)_{1} z_{k}(j)$；$b^{(0)}$ 是对 query 前景的 soft predictions的均值 ：$b^{(0)}=\frac{1}{|\Psi|} \sum_{j \in \Psi} p_{\mathcal{Q}}(j)_{1}$。

B/F 比例 $\pi$ 的联合估计：当没有先验知识时，RePRI 使用 $\widehat{p}_{\mathcal{Q}}$ 来联合学习 $\pi$ 和分类器的参数，这时 $\mathcal{D}_{\mathrm{KL}}$ 可以被视为 self-regularization 来防止模型的 marginal distribution 发生偏移。具体实现中，只在初始化后在之后的某一轮迭代 $t_{\pi}$ 更新一次 $\pi$ 即可，即

$$\pi^{(t)}= \begin{cases}\widehat{p}_{\mathcal{Q}}^{(0)} & 0 \leq t \leq t_{\pi} \\
\hat{p}_{\mathcal{Q}}^{\left(t_{\pi}\right)} & t>t_{\pi}\end{cases}$$

实验结果：

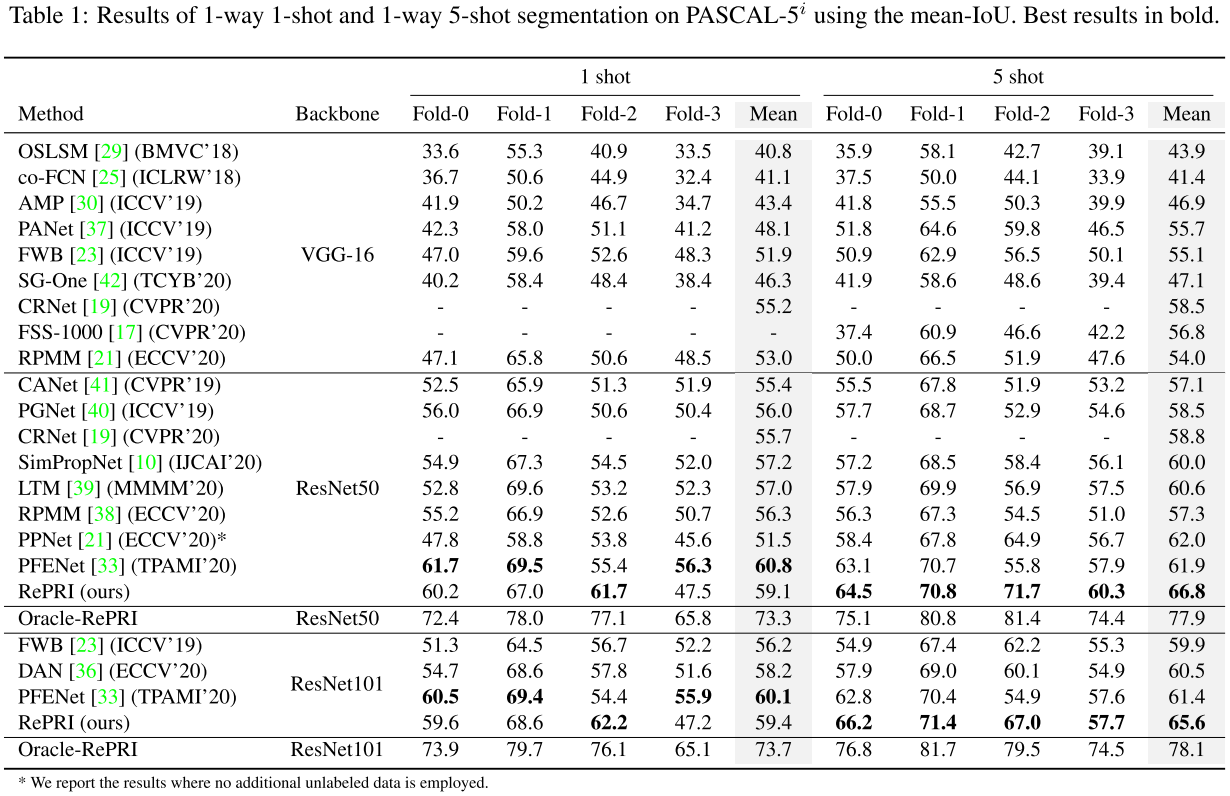
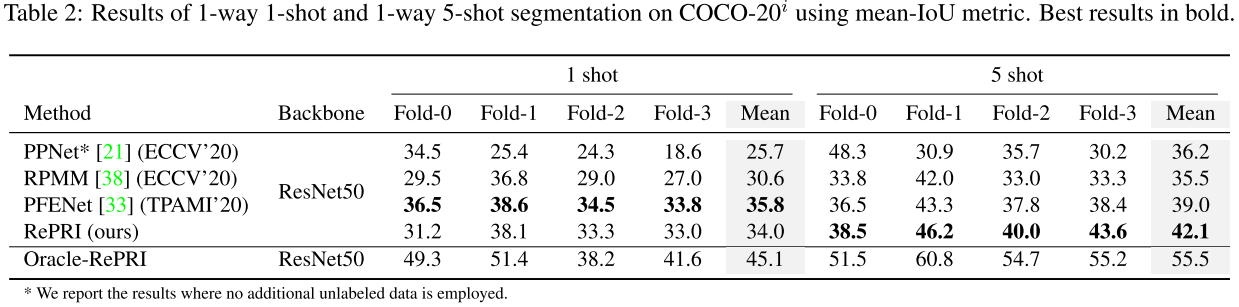
可以看到在 5-shot 上 RePRI 取得了全面的 SOTA。本文同样做了包含 (1) 训练时采用 1-shot task、测试时用 1-\5-\10-shot task；(2) cross-domain 等实验。具体请看原论文。

Self-Guided and Cross-Guided Learning for Few-Shot Segmentation

CVPR 2021 | link | github

本文同样提出常用的 masked Global Average Pooling (GAP) 来将 support 图像转换为特征向量的方式会导致有区分性的信息因为求均值操作而损失。另外，当 shot 数量不为 1 时，常用的对所有 support 向量求均值会强制使得所有的 support 图像贡献相同，而不同的 support 图像的对于表示类别的贡献实际上是不同的。

为了解决这两个问题，本文提出 Self-Guided and Cross-Guided Learning (SCL)，首先用初始原型来对 support 图像做初始预测，预测覆盖和没有覆盖到的前景区域被用 masked GAP 编码成 primary 和 auxiliary support 向量来在 query 图像的分割上取得更好表现。同时，针对 shot 数量不为 1 的场景，本文提出 Cross-Guided Module (CGM) 来使用其他有标注 support 图像评估每张 support 图像的预测质量，使高质量的 support 图像能够对最终的融合做出更大的贡献。相比 attention 等复杂的方法，CGM 无需重新训练模型，可以直接在 inference 时被应用来提升最终的表现。SCL 遵循 episodic training 的方式，总损失为 $\mathcal{L}=\mathcal{L}_{c e}^{s 1}+\mathcal{L}_{c e}^{s 2}+\mathcal{L}_{c e}^{q}$，前两项来自 support set 的 Self-Guided Learning，后一项来自 query set。

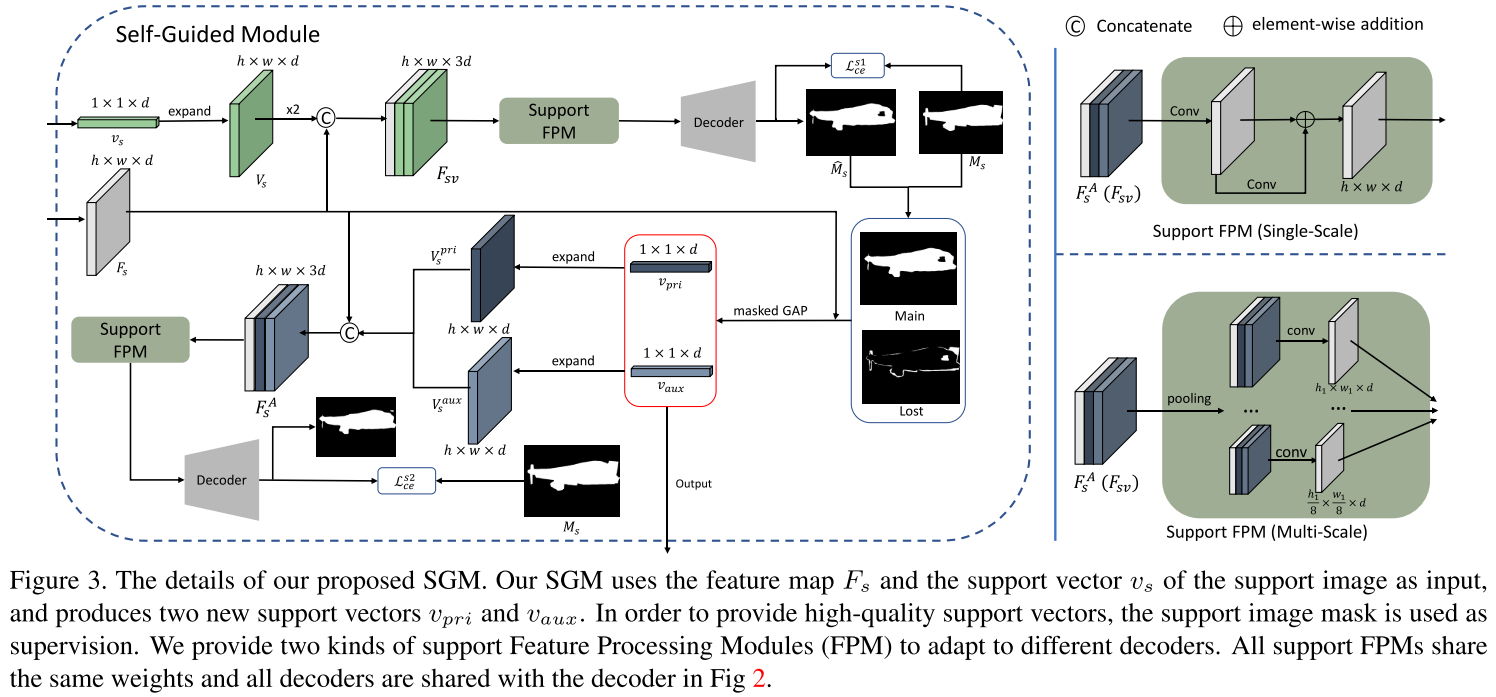
Self-Guided Learning on Support Set：这里首先以 1-shot 为例。用 masked GAP 获得的初始 support 向量 $\mathcal{v}_s$ 被扩展成和 support 特征图 $F_s$ 同样大小的 $V_s$，然后拼接得到新的特征图 $F_{sv} = \text{Concat}([F_s, V_s, V_s])$。通过将 $F_{sv}$ 输入到 support FPM 和 decoder，可以得到support 图像的概率图 $P_{s1} = \text{softmax}(\mathcal{D}(FPM_s(F_{sv})))$，其中 $\mathcal{D}(\cdot)$ 指 decoder。由于 SCL 是一个即插即用的模块，因此 support FPM 和 decoder 的设计遵循所选择的小样本分割 baseline。本文的实验部分选择插入到两种 baseline 中：(1) CANet (CVPR 2019)，其 decoder 是 single-scale 结构的，因此 SCL 也采用 single-scale support FPM；(2) PFENet (TPAMI 2020)，其 decoder 是 multi-scale 结构的，因此 SCL 也采用 multi-scale support FPM。single-scale 和 multi-scale 的 support FPM 结构如上图右边所示。

使用预测的 mask $\hat{M_s} = \text{argmax}(P_{s1})$ 和 ground-truth mask $M_s$，可以得到 primary support 向量 $\mathcal{v}_{pri}$ 和 auxiliary support 向量 $\mathcal{v}_{aux}$，前者代表预测正确的实际前景信息，后者代表预测错误的实际前景信息。换句话说，$\mathcal{v}_{pri}$ 保持着主要的 support 信息，而 $\mathcal{v}_{aux}$ 包含用 $\mathcal{v}_s$ 无法预测的、损失的重要信息。为了保证 $\mathcal{v}_{pri}$ 能够从 support 的特征图收集到大多数的信息，对 $P_{s1}$ 施加交叉熵得到 $\mathcal{L}_{c e}^{s 1}$：

$$\mathcal{L}_{c e}^{s 1}=-\frac{1}{h w} \sum_{i=1}^{h w} \sum_{c_{j} \in{0,1}}\left[M_{s}(i)=c_{j}\right] \log \left(P_{s 1}^{c_{j}}(i)\right)$$

接下来，$\mathcal{v}_{pri}$ 和 $\mathcal{v}_{aux}$ 也被扩展并与 $F_s$ 拼接得到 $F^A_{s} = \text{Concat}([F_s, V^{pri}_s, V^{aux}_s])$，然后得到 $P_{s2} = \text{softmax}(\mathcal{D}(FPM_s(F^A_{s})))$。为了确保集成 $\mathcal{v}_{pri}$ 和 $\mathcal{v}_{aux}$ 能够得到精准的分割 mask，同样施加交叉熵得到 $\mathcal{L}_{c e}^{s 2}$：

$$\mathcal{L}_{c e}^{s 2}=-\frac{1}{h w} \sum_{i=1}^{h w} \sum_{c_{j} \in{0,1}}\left[M_{s}(i)=c_{j}\right] \log \left(P_{s 2}^{c_{j}}(i)\right)$$

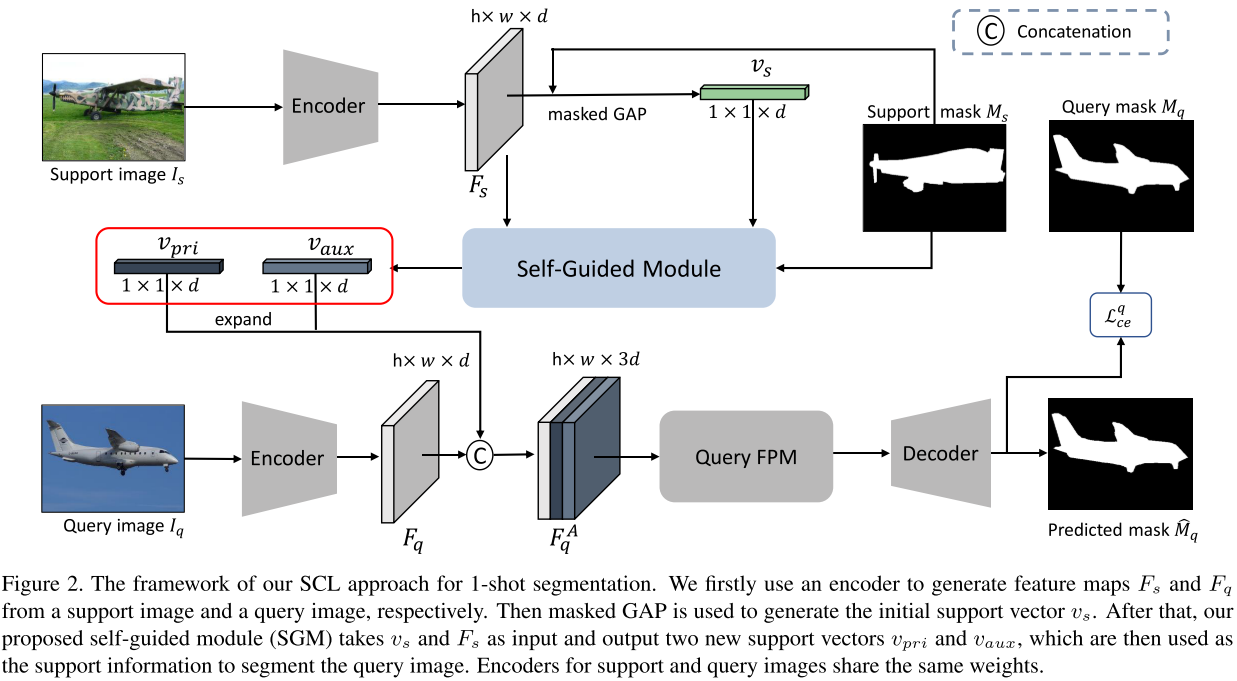
Training on Query Set：对于 query 的特征图 $F_q$，流程为 $F^A_{q} = \text{Concat}([F_q, V^{pri}_q, V^{aux}_q])$，其中 $V^{pri}_q$ 和 $V^{aux}_q$ 是 $\mathcal{v}_{pri}$ 和 $\mathcal{v}_{aux}$ 扩展大小得到；$P_{q} = \text{softmax}(\mathcal{D}(FPM_q(F^A_{q})))$，注意这里有一个单独的 query FPM $FPM_q$ 而非 $FPM_s$。同样计算交叉熵得到 $\mathcal{L}_{c e}^{q}$：

$$\mathcal{L}_{c e}^{q}=-\frac{1}{h w} \sum_{i=1}^{h w} \sum_{c_{j} \in{0,1}}\left[M_{q}(i)=c_{j}\right] \log \left(P_{q}^{c_{j}}(i)\right)$$

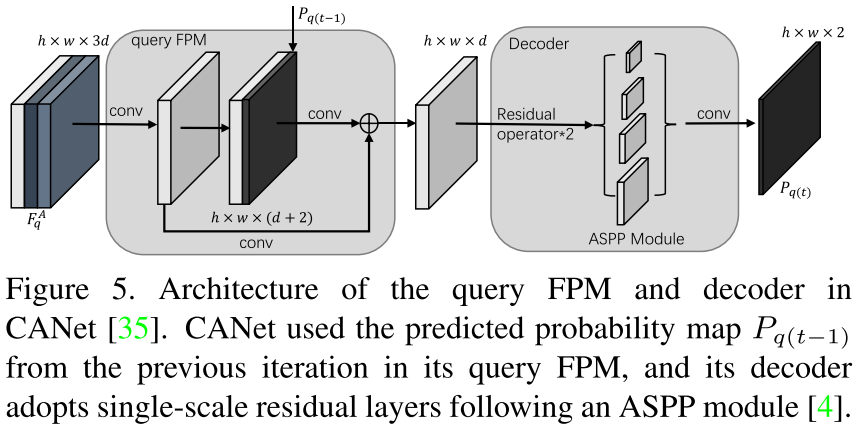
Cross-Guided Multiple Shot Learning：当 shot 数 > 1 时，对于第 k 张 support 图像，首先将其作为 support 图像，将所有 K 张 support 图像作为 query 图像来输入到所提出的面向 1-shot 的模型中。对于第 i 张 support 图像，得到在第 k 张图像的支持下的预测 mask $\hat{M}_{s}^{i \mid k}$。因为第 i 张 support 图像的 ground-truth mask $M_s^i$ 是可得的，因此可以用预测和 ground-truth 的 masks 的 IOU 来计算一个置信度：

$$U_{s}^{k}=\frac{1}{K} \sum_{i=1}^{K} \text{IOU}\left(\hat{M}_{s}^{i \mid k}, M_{s}^{i}\right)$$

则对于给定的 query 图像的最终预测 score map：

$$\hat{P}_{q}=\text{softmax}\left(\frac{1}{K} \sum_{k=1}^{K} U_{s}^{k} \mathcal{G}\left(I_{q} \mid I_{s}^{k}\right)\right)$$

可以看到有更大的 $U_{s}^{k}$ 的 support 图像对于最终的预测有更大的贡献。

实验结果：

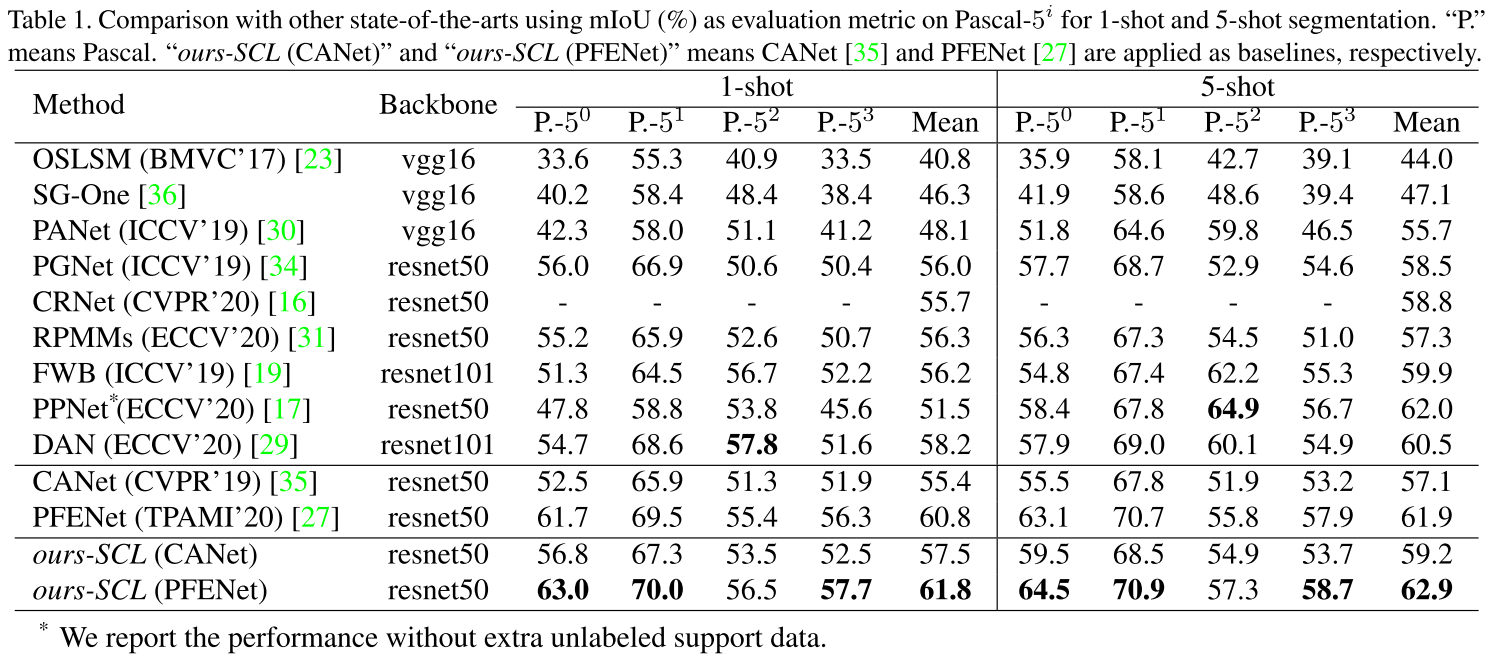
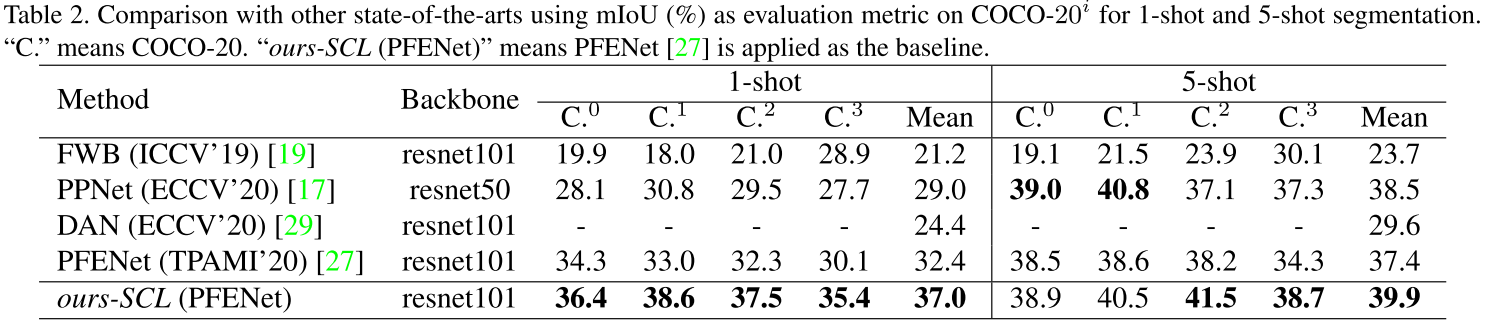
Adaptive Prototype Learning and Allocation for Few-Shot Segmentation

CVPR 2021 | link | github

本文认为虽然相比需要用稠密 affinity 矩阵来解决欠约束的像素匹配问题而容易过拟合的 affinity learning，常用的 prototypical learning 能够比单纯的像素特征更加鲁棒，但是仅用一个 prototype 不足以表示包含空间信息在内的所有信息。特别地，本文希望能够根据图像内容自适应地调整 prototypes 的数量和空间范围，从而能够更好地处理物体在尺寸和形状上的变化。例如对一个尺寸较小的物体，可能一个或少量 prototypes 就足够了；而对于尺寸较大的物体，可能需要更多的 prototypes 来表示所有重要的信息。

因此，本文提出 Adaptive Superpixel-guided Network (ASGNet)，包含 superpixel-guided clustering (SGC) 和 guided prototype allocation (GPA) 两个模块用于提取和分配多个 prototypes。SGC 模块在 support 图像上进行快速的、基于特征的 superpixel 提取，得到的 superpixel centroids 可以被视为 prototypical 特征，同时 superpixel 的数量和形状都是适应于图像内容的，因此得到的 prototypes 是自适应的。GPA 模块用一个 attention-like 机制来讲最相关的 support prototype 特征分配给 query 图像中的每个像素。最后，ASGNet 使用 PFENet (TPAMI 2020) 中的特征增强结构并建立一个 FPN-like top-down 结构来引入 multi-scale 信息。当 shot 数大于 1 时，每张 support 图像都可以得到一组 prototypes，所有的 prototypes 被一块作为 GPA 的选择范围。

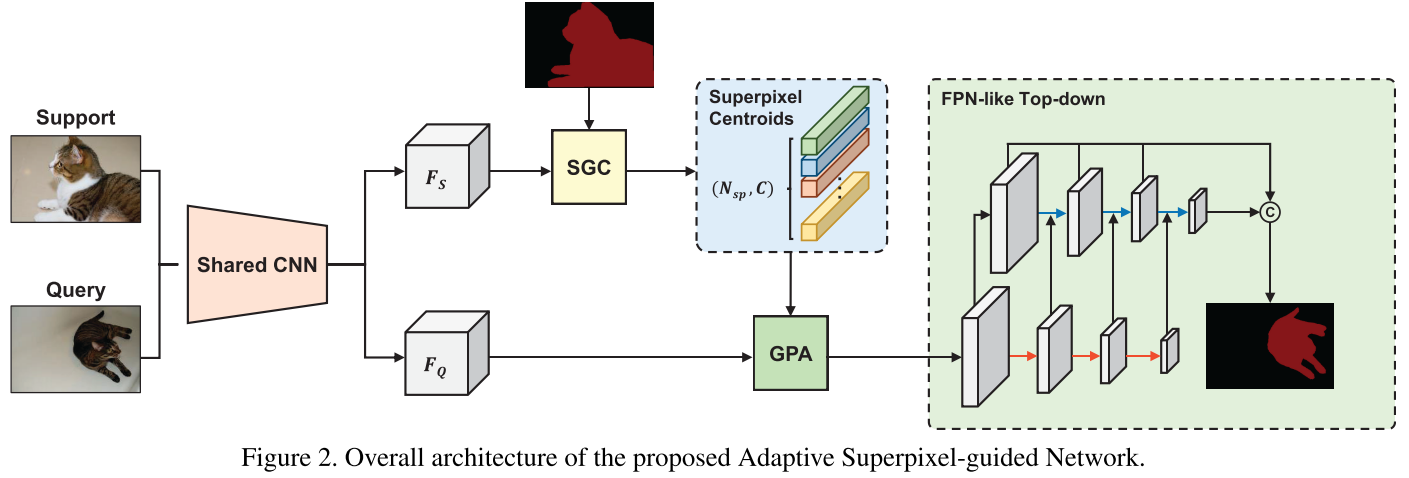
Superpixel-guided Clustering：受到 maskSLIC (2016), Superpixel sampling networks (ECCV 2018) 等工作的启发，SGC 模块被用于将特征图用聚类的方式集成到多个 superpixel centroids 中。给定 support 特征 $F_s \in \mathbb{R}^{c \times h \times w}$ 和 support mask $M_s \in \mathbb{R}^{h \times w}$，假设已经获得初始 superpixel 种子，SGC 首先将 support 特征图上每个像素的坐标的值进行放缩后和特征图进行拼接，从而引入位置信息。之后用 support mask 来筛除背景信息，这样我们获得 $F_s^{`} \in \mathbb{R}^{(c+2) \times N_m}$，$N_m$ 是在 support mask 中的像素的数量（注意这里我们对变量及其维度表示和原论文略有差别，我在阅读了源码后觉得这样表述会更清晰）。同样，我们也将初始 superpixel 种子的特征和其值放缩后的坐标拼接，有 $S^{0} \in \mathbb{R}^{(c+2) \times N_{sp}}$（$N_{sp}$ 是 superpixel 的数量。获得初始种子的方法见本节最后一段）。接下来，SGC 通过迭代式的方法更新 superpixel-based prototypes：在第 $t$ 轮迭代，首先计算每个像素 $p$ 和所有 superpixels 的 association map $Q^t$：

$$Q^t_{pi} = e^{- || F^{`}_p - S^{t-1}_i ||^2}$$

接下来，新的 superpixel centroids 被更新为 masked 特征的加权和：

$$S^t_i = \frac{1}{\sum_pQ^t_{pi}} \sum^{N_m}_{p=1} Q^t_{pi} F^{`}_p$$

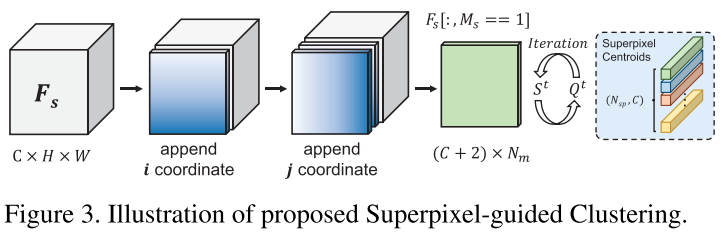
通常 superpixel 算法通过将图像划分为均匀大小的 grid cell 来选取初始种子（i.e., superpixel），但由于只需要从前景区域来初始化种子，本文参考 maskSLIC (2016) 来迭代式地安置每个初始种子，流程如下图所示。

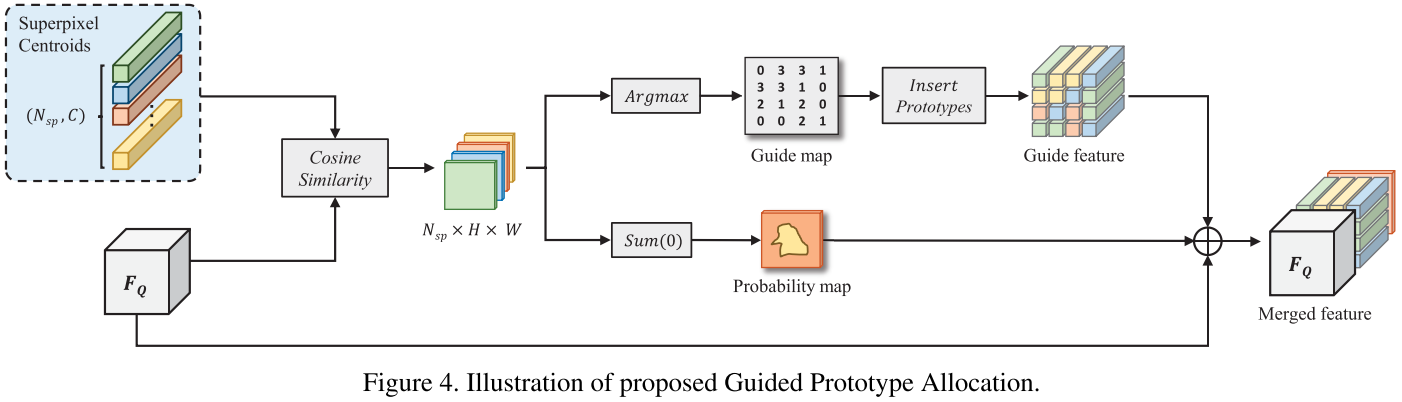
Guided Prototype Allocation：首先计算每个 prototype 和 query 特征每个位置的 cosine 相似度 $C^{x,y}_i$，这个相似度信息被输入到一个双分支结构。第一个分支计算每个位置的像素和哪个 prototype 最相似：

$$G^{x,y} = \text{argmax}_{i \in {0, \dots, N_{sp}}} C^{x,y}_i$$

根据得到的 guide map $G \in \mathbb{R}^{h \times w}$，可以通过将对应 prototype 放到 guide map 的每个位置得到 guide feature $F_G \in \mathbb{R}^{c \times h \times w}$。第二个分支将相似度信息 $C$ 在所有的 superpixels 相加来得到概率图 $P$。最终将 $P$、$F_G$ 和原本的 query 特征 $F_Q$ 拼接并过 $1 \times 1$ 卷积得到 refined query 特征 $F^{`}_Q$。

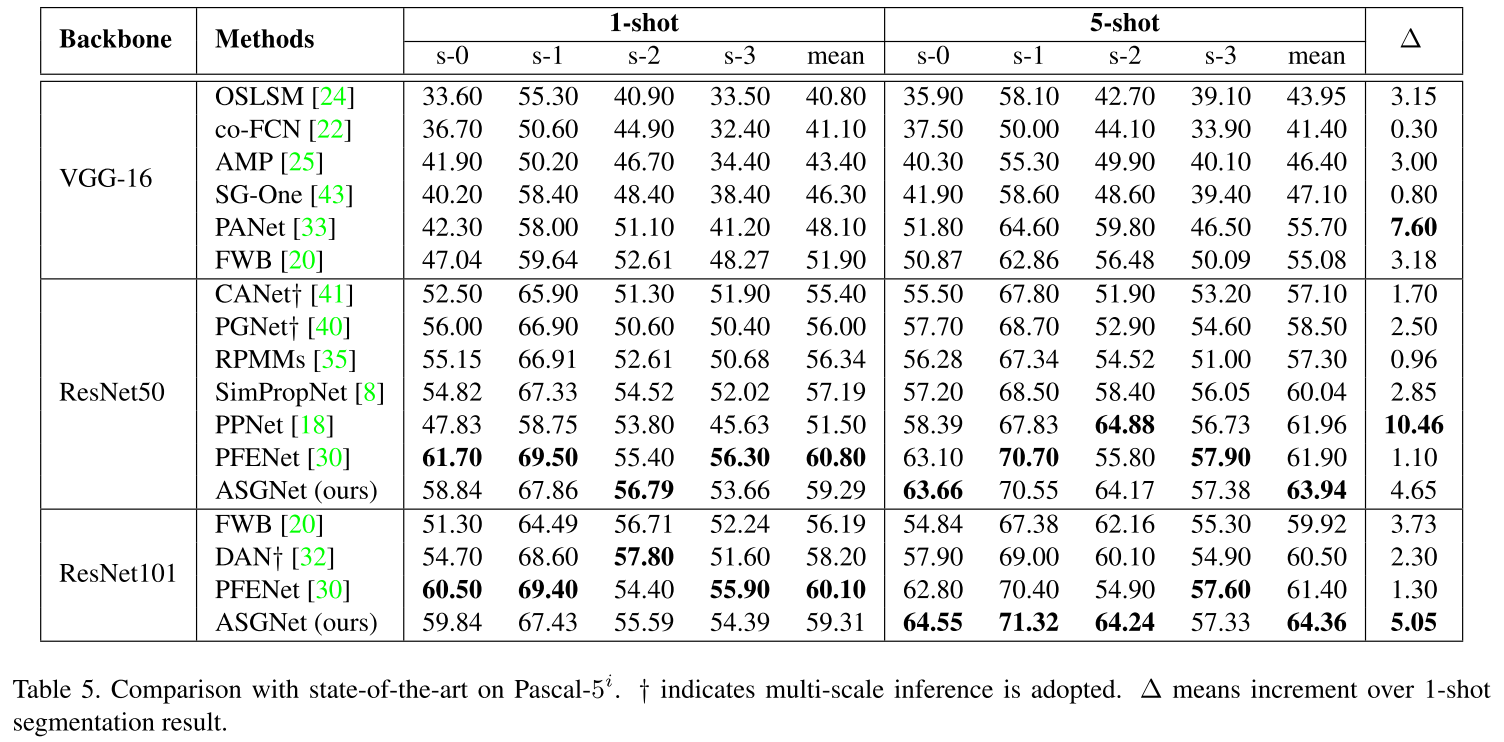
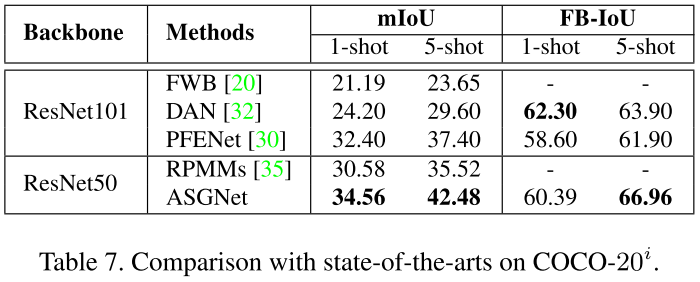
实验结果：

Mining Latent Classes for Few-shot Segmentation

ICCV 2021 | arxiv | github：只给了一个在基础 metric-based 方法上做了些修改的 baseline，没有给论文所提出的方法的代码！

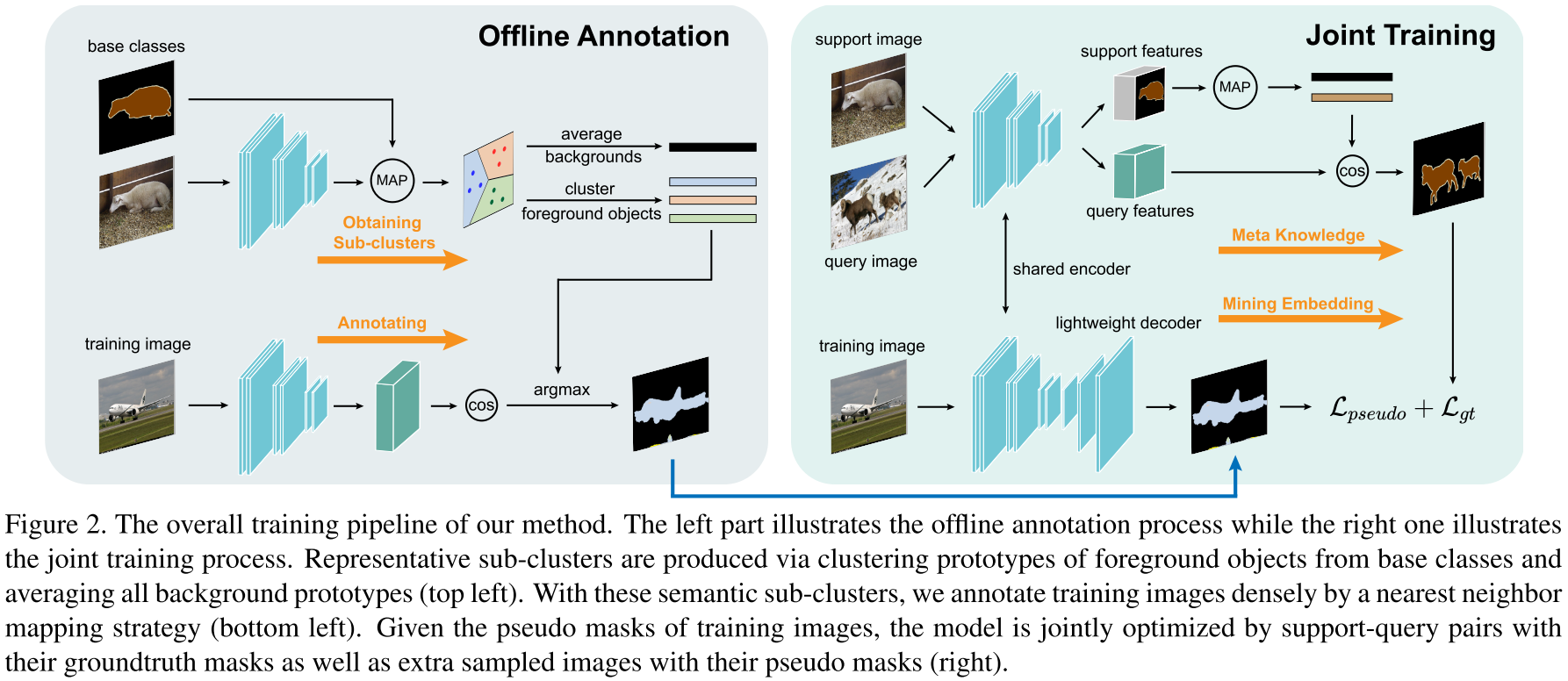
该论文的所谓“代码开源”令人不满，因此只做简单笔记。在 PPNet (ECCV 2020) 等工作的基础上，本文的方法：

1. 将元训练分为离线标注（Offline Annotation）和协同训练（Joint Training）两个阶段。离线标注阶段，模型在所有训练图像得到的所有类别的原型集合（数量上限为图像数 $\times$ 类别数，当然不是每张图像都含所有类别的物体）中通过 K-Means 聚类产生 $K$ 个簇心，同时直接对所有代表背景的原型求均值得到全局背景原型，从而得到 $K+1$ 个新原型，用于给所有训练图像的所有像素用 cosine 相似度打 $K+1$ 类的伪标签（pseudo masks）。除开背景类别外，另外 $K$ 个聚类所得到的类不代表具体的物体种类，而是表示类别的一些共同特征（例如，“马”和“牛”都有的“四足动物”特征）；协同训练阶段采用 episodic training，并额外加了一个分支来用交叉熵训练预测 pseudo masks。该分支由三层带 BN 和 ReLU 的卷积构成，另外考虑到 pseudo masks 的噪声会在训练后期影响性能，因此模型参数更新时计算指数移动平均值（exponential moving average），使模型参数的更新更稳定。
2. 由于学习新类时样本量过少，因此对用于像素二分类的背景和前景原型都分别进行纠偏。背景原型纠偏：在训练阶段采用指数移动平均值来不断用当前的背景原型来更新全局背景原型，在推断时用该全局背景原型和 support 的背景原型线性求和；前景原型纠偏：给定一张 support 图像，根据图像嵌入的 cosine 相似度选择前 N 张相关图像（一个问题就是这里没说相关图像是从哪个集合选），然后根据 support 的前景原型来挑选 K 个最相关的区域原型（这里也没说所谓的“区域”具体是怎么得到的），所有的嵌入通过 ResNet-50/101 的第三层的输出的平均池化得到。之后通过计算前景原型和区域原型的相似度来以加权求和的方式更新前景原型。

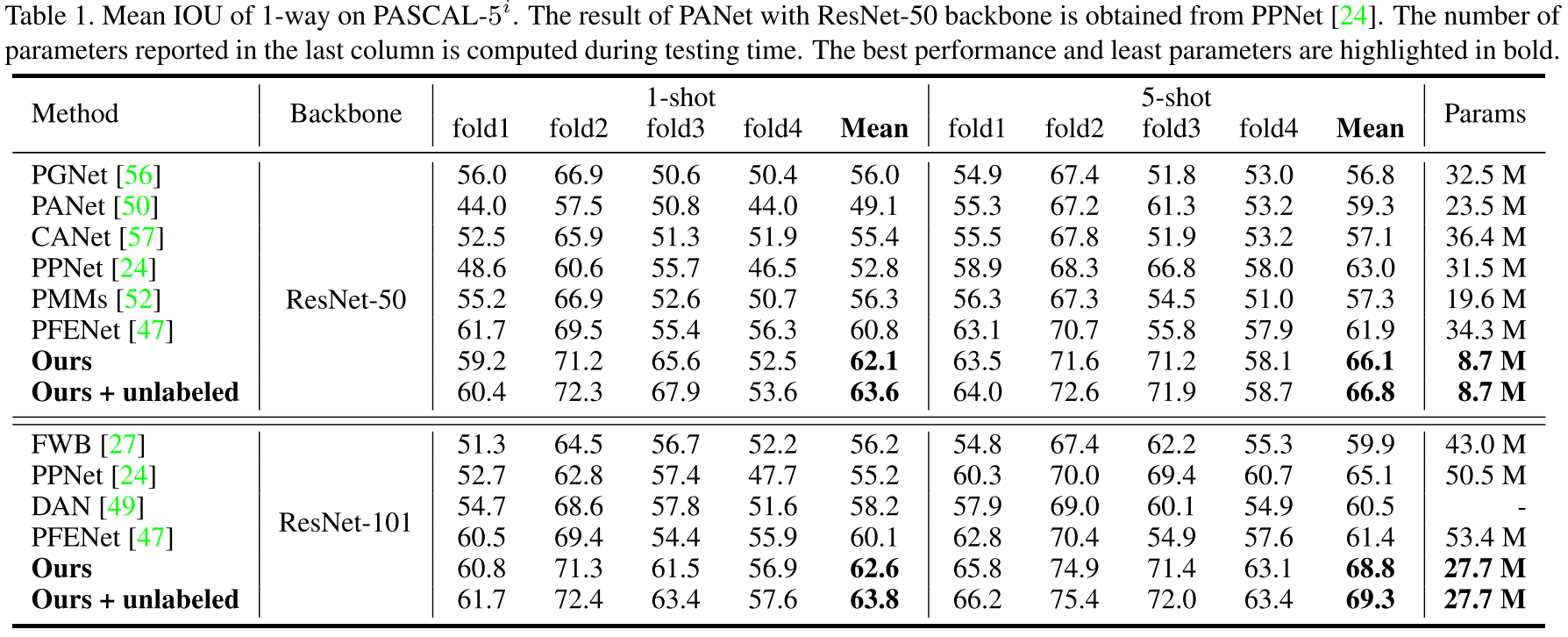
实验结果就放一张在 PASCAL-5$^i$ 上的 SOTA 对比好了。虽然实验做的还比较详细，但是不给方法代码导致结果可信度要打一个问号。

Few-Shot 3D Point Cloud Semantic Segmentation

CVPR 2021 | link | github

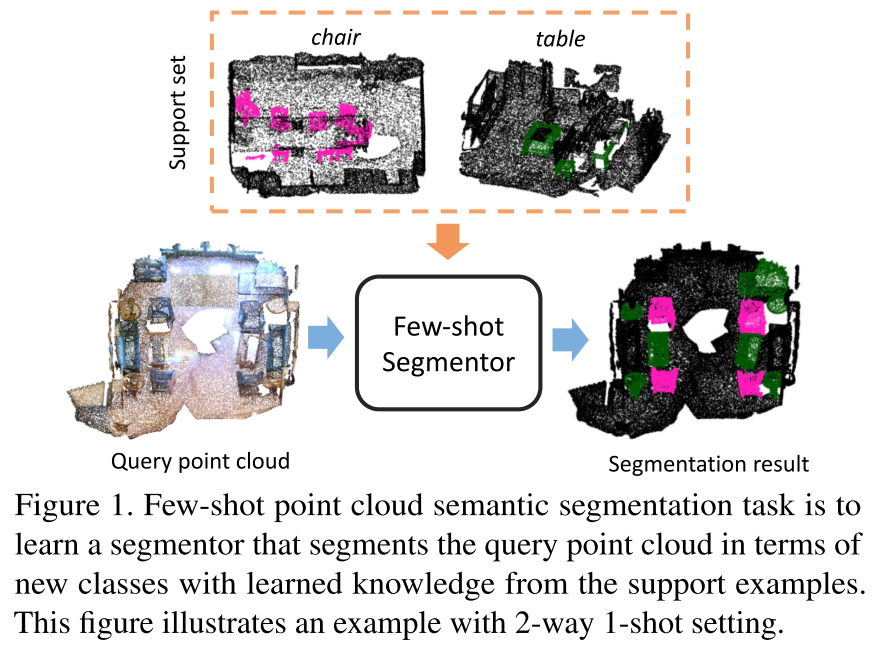
第一篇做小样本 3D 点云语义分割的论文。相比 2D 图像，点云更加无结构和无序，因此做语义分割的难度会更大。任务定义如上图所示，基本就是把 2D 数据换成 3D 点云。方法上，本文提出了 attention-aware multi-prototype transductive inference 框架。其包含以下三点：

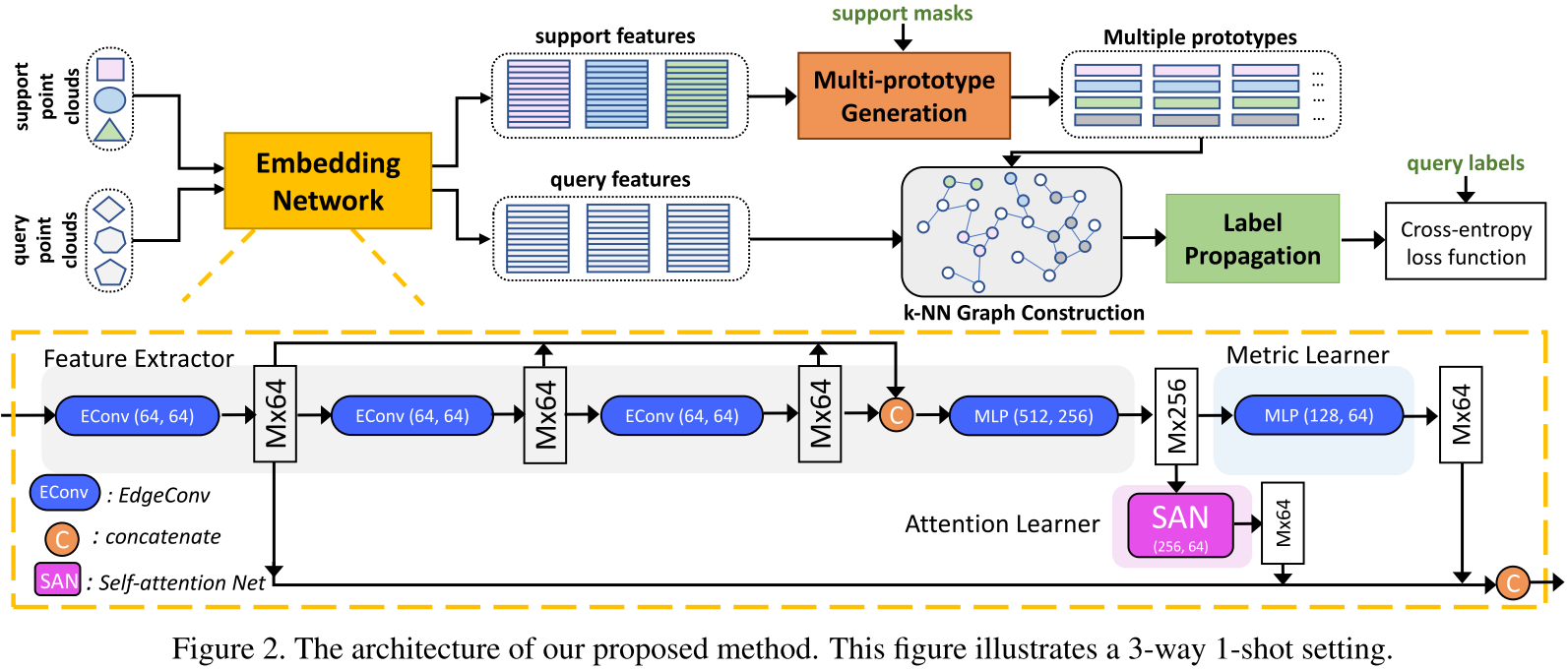
embedding network：对标 2D 视觉中的 CNN 等 backbone 网络。论文提出这个网络需要满足 (1) 能够根据局部上下文编码几何结构；(2) 能够根据全局上下文编码点云的语义信息和它们间的语义关系；(3) 能够快速适应不同的小样本任务。因此，本文提出一种 attention-aware multi-level feature learning network 来结合局部几何特征、全局语义特征和 metric-adaptive 特征。具体来说，该网络由三部分组成：(1) feature extractor，选用动态图 CNN 架构的 DGCNN (ACM Trans. Graph. 2019) 来得到局部几何特征（第一个 EdgeConv 层的输出）和语义特征（整个 feature extractor 的输出）；(2) attention learner，选用了 self-attention network (SAN)；(3) metric learner，选用了 MLP 的堆叠并以一个相对更大的学习率更新。

multi-prototype generation：对于 support set 中 $N+1$ 类的每一个，都通过聚类生成 $n$ 个 prototypes。具体地，$n$ 个种子点通过 farthest point sampling 被从 support 点中采样得到。直觉上来说，如果 embedding space 学得够好，这个空间中最远的那些点能够可以内在地表示一个类别的不同视角。之后，我们计算其他点和这些种子点的距离并根据最近邻原则分配，最后计算每个簇的均值作为 prototypes。

transductive inference：该方法首先构建了一张包含 $n \times (N+1)$ 个 prototypes 和 $T \times M$ 个 query 点、总计 $V = n \times (N+1) + T \times M$ 个节点的 k-NN graph。稀疏邻接矩阵 $\mathbf{A} \in \mathbb{R}^{V \times V}$ 通过计算每个点和其 $k$ 个最近邻的高斯相似度得到。为了让邻接矩阵是非负且对称的，有 $\mathbf{W} = \mathbf{A} + \mathbf{A}^{T}$，并进一步进行正则化有 $\mathbf{S} = \mathbf{D}^{-1/2}\mathbf{W}\mathbf{D}^{-1/2}$。同时定义标签矩阵 $\mathbf{Y} \in \mathbb{R}^{V \times (N+1)}$，其中对应有标签 prototypes 的行是 one-hot ground-truth 标签，其余为零向量。给定 $\mathbf{S}$ 和 $\mathbf{Y}$，标签传播有解析解 $\mathbf{Z}^{*} = (\mathbf{I} - \alpha \mathbf{S})^{-1}\mathbf{Y}$。最后每个点云对应的预测通过 softmax 后用交叉熵计算损失。

数值的实验结果如下表所示。原论文还有一些 ablation study 和分割结果的可视化。