DSANet: Dual Self-Attention Network for Multivariate Time Series Forecasting

paper code poster slide

Background

Multivariate time series forecasting has attracted wide attention in areas, such as system, traffic, and finance. The difficulty of the task lies in that traditional methods fail to capture complicated non-linear dependencies between time steps and between multiple time series. Recently, recurrent neural network and attention mechanism have been used to model periodic temporal patterns across multiple time steps. However, these models fit not well for time series with dynamic-period patterns or nonperiodic patterns. In this paper, we propose a dual self-attention network (DSANet) for highly efficient multivariate time series forecasting, especially for dynamic-period or nonperiodic series. Experiments on real-world multivariate time series data show that the proposed model is effective and outperforms baselines.

Model Overview

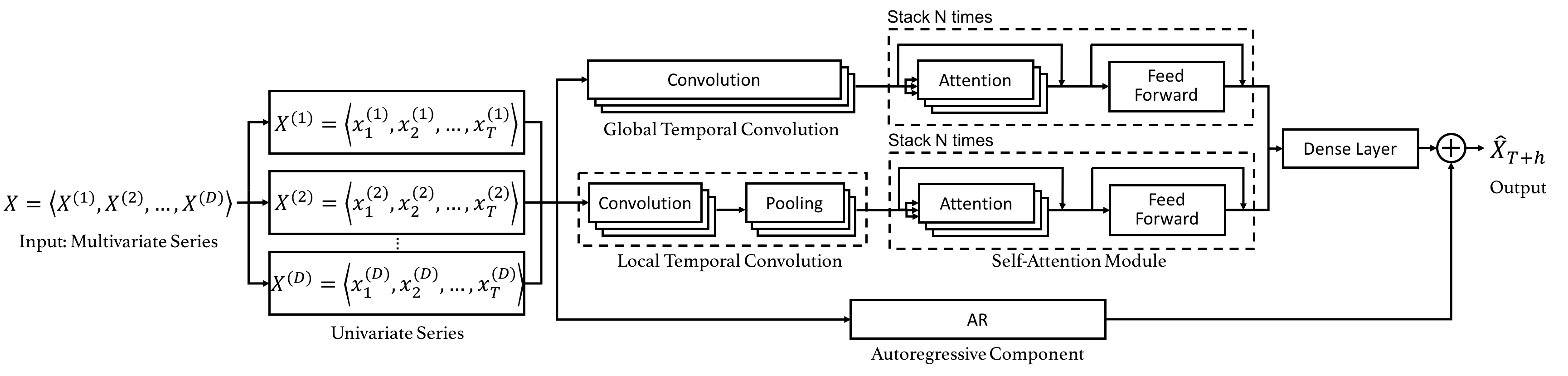
• Global Temporal Convolution: First, DSANet applies 1D convolution over all time steps to extract global temporal patterns for univariate time series.
• Local Temporal Convolution: Considering that time steps with a shorter relative distance have a larger impact on each other, DSANet uses another 1D convolution with shorter length of filters to model local temporal patterns.
• Self-attention Module: To capture the dependencies between different series, a self-attention module inspired by the Transformer (Vaswani et al., 2017) is applied.
• Autoregressive Component: To address the drawback that the scale of neural network output is not sensitive to that of input, the final prediction of DSANet is a mixture of the non-linear component and a classical autoregressive model.

Experiment Results

We conduct our experiments on a large multivariate time series dataset, which contains the daily revenue of geographically close gas stations. Data visualization analysis is performed to ensure that the data set does not contain distinct repetitive patterns. Please check the paper for the details of the experiment settings and further analysis.

Evaluation Results

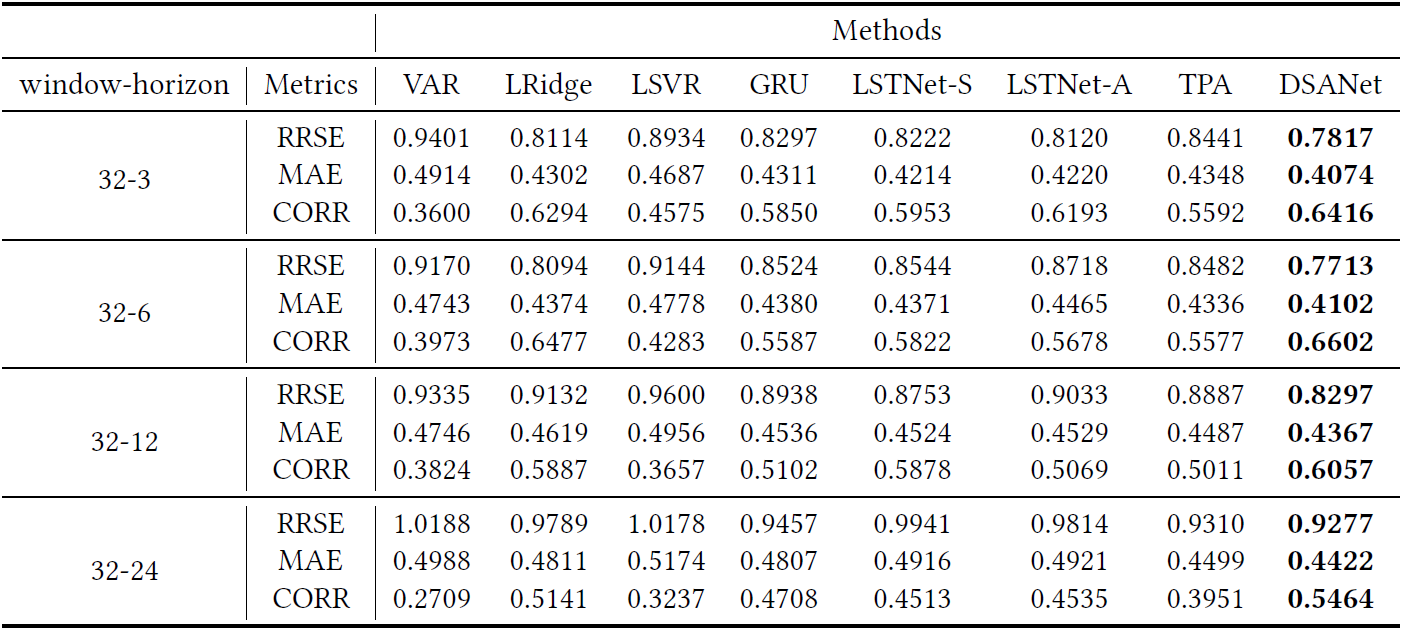
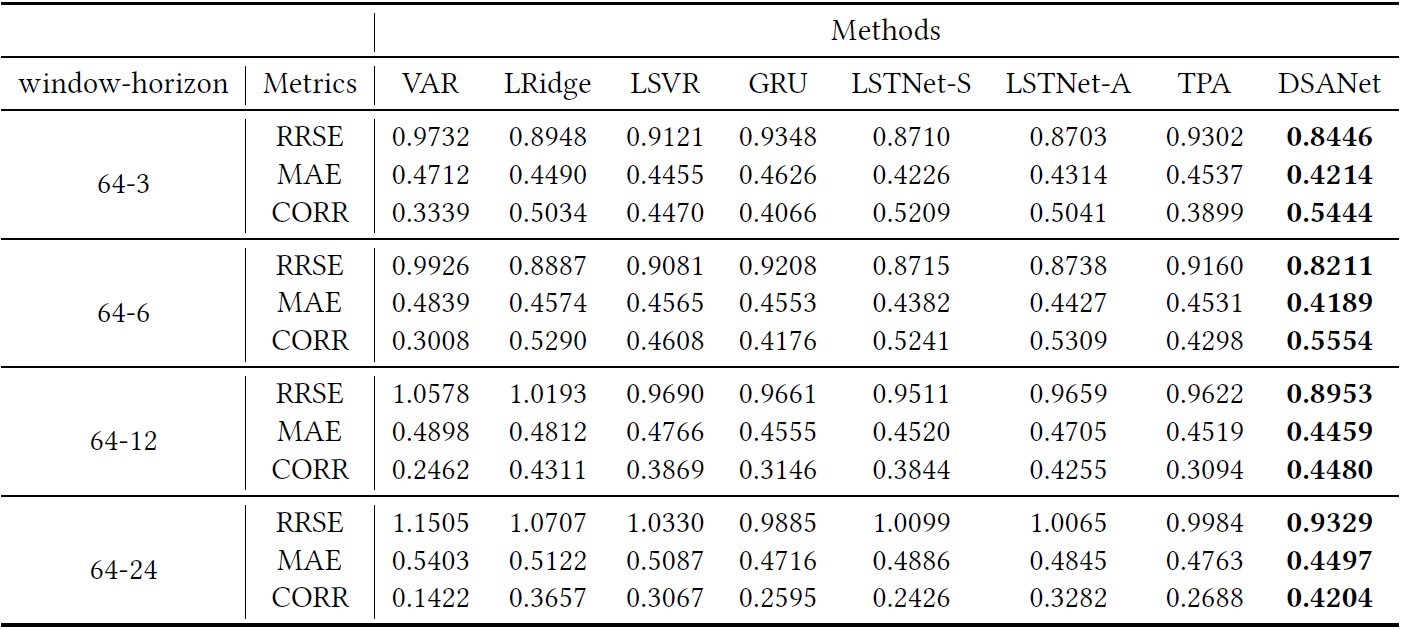
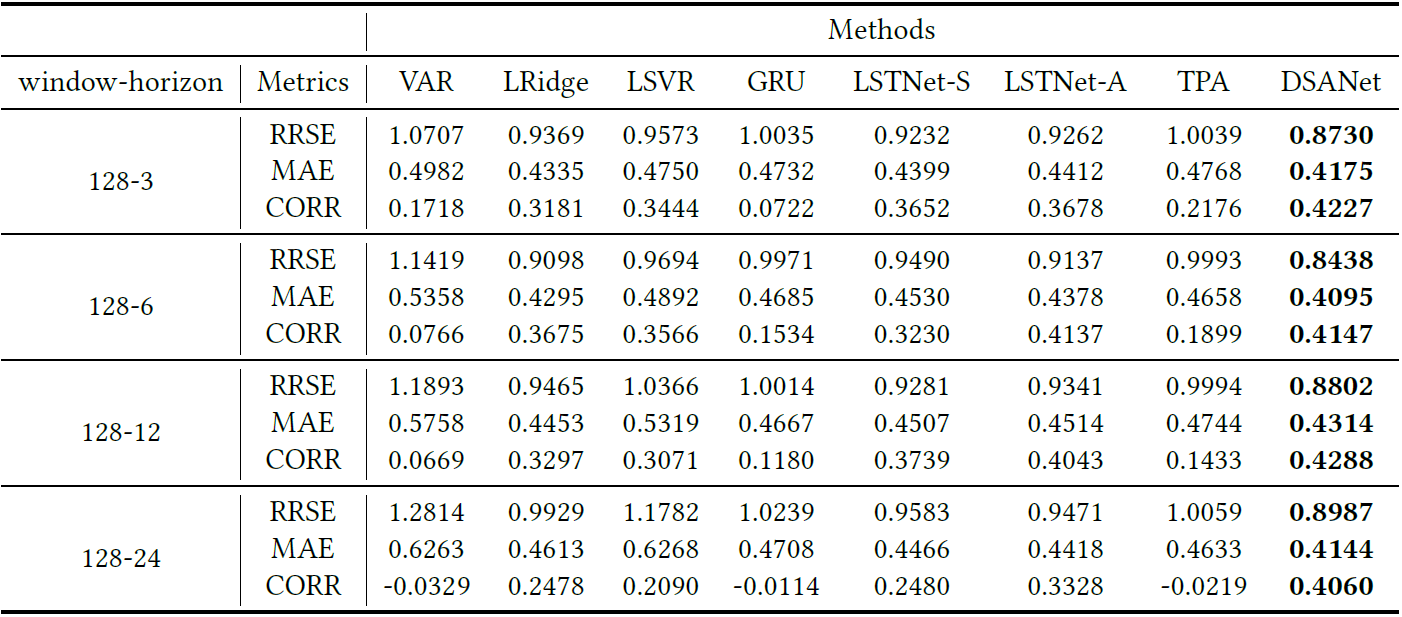
Each row in the table compares the results of all methods in a particular metric with a specific window-horizon pair, and each column shows the results of a specific method in all cases. Boldface indicates the best result of each row in a particular metric.

With window = 32:

With window = 64:

With window = 128:

Ablation Study

To justify the efficiency of our architecture design, we conduct a careful ablation study. Specifically, we remove each of the components one at a time in our DSANet model:

• DSAwoGlobal: Remove the global temporal convolution branch.
• DSAwoLocal: Remove the local temporal convolution branch.
• DSAwoAR: Remove the autoregressive component.

With window = 32:

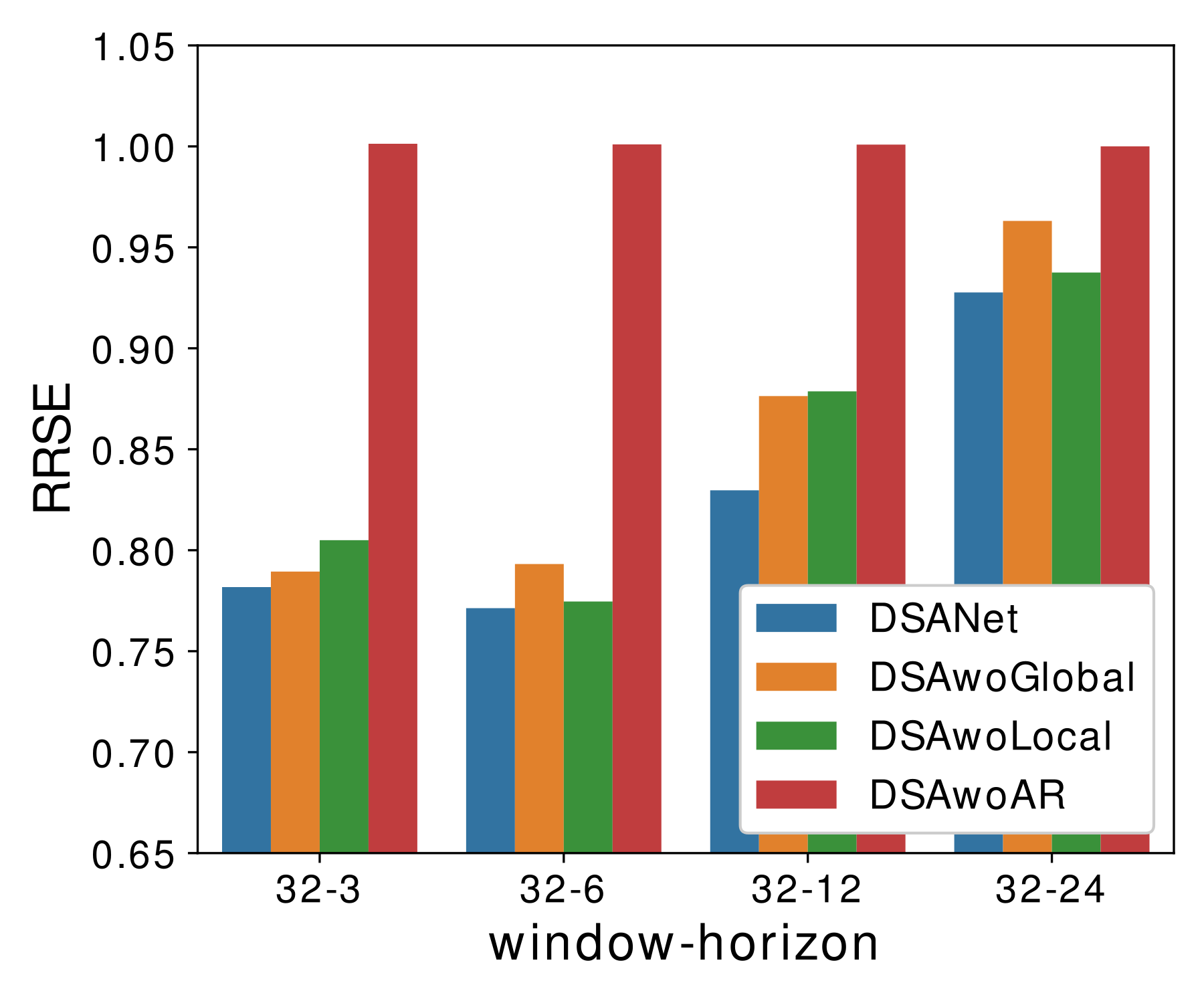
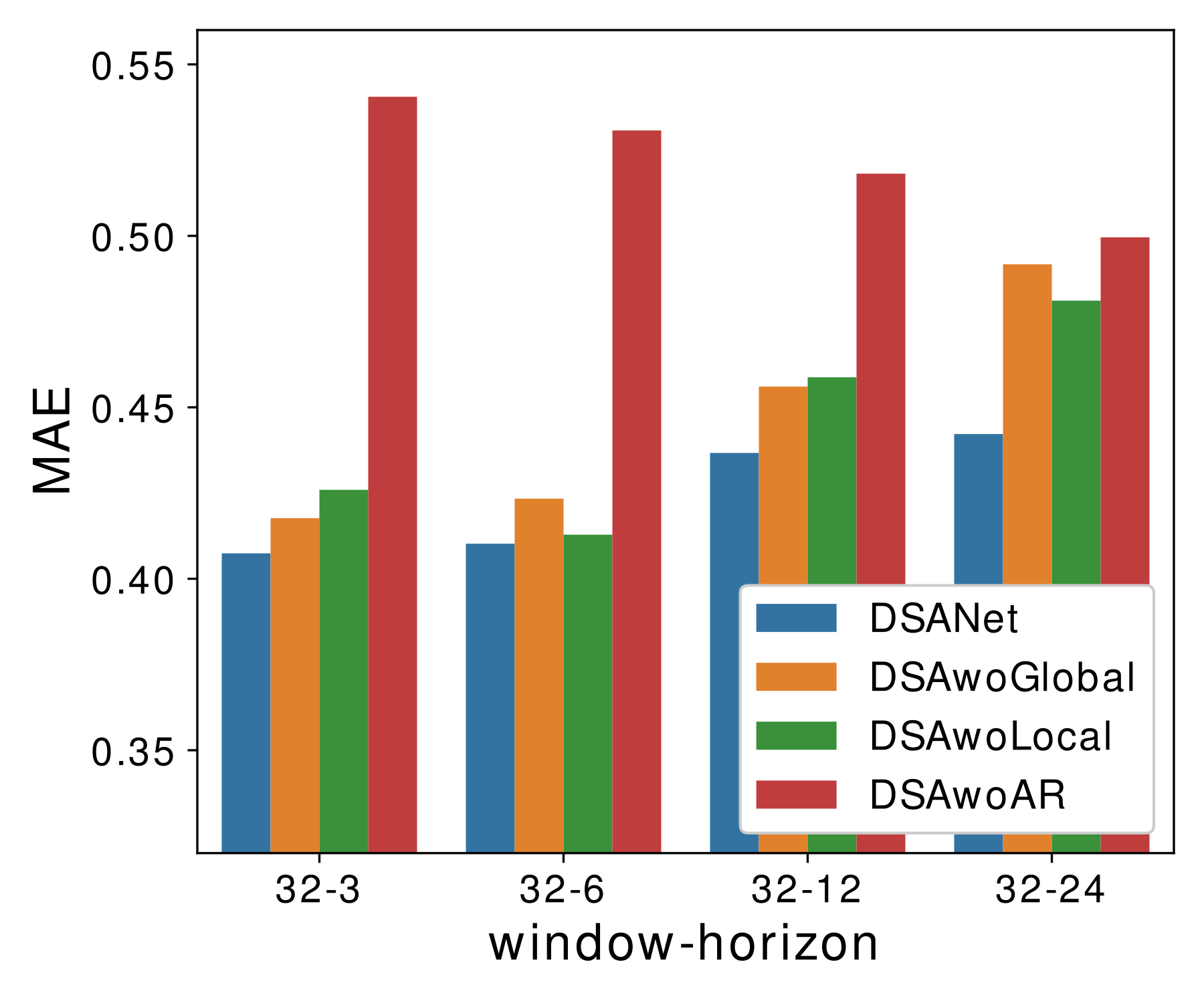
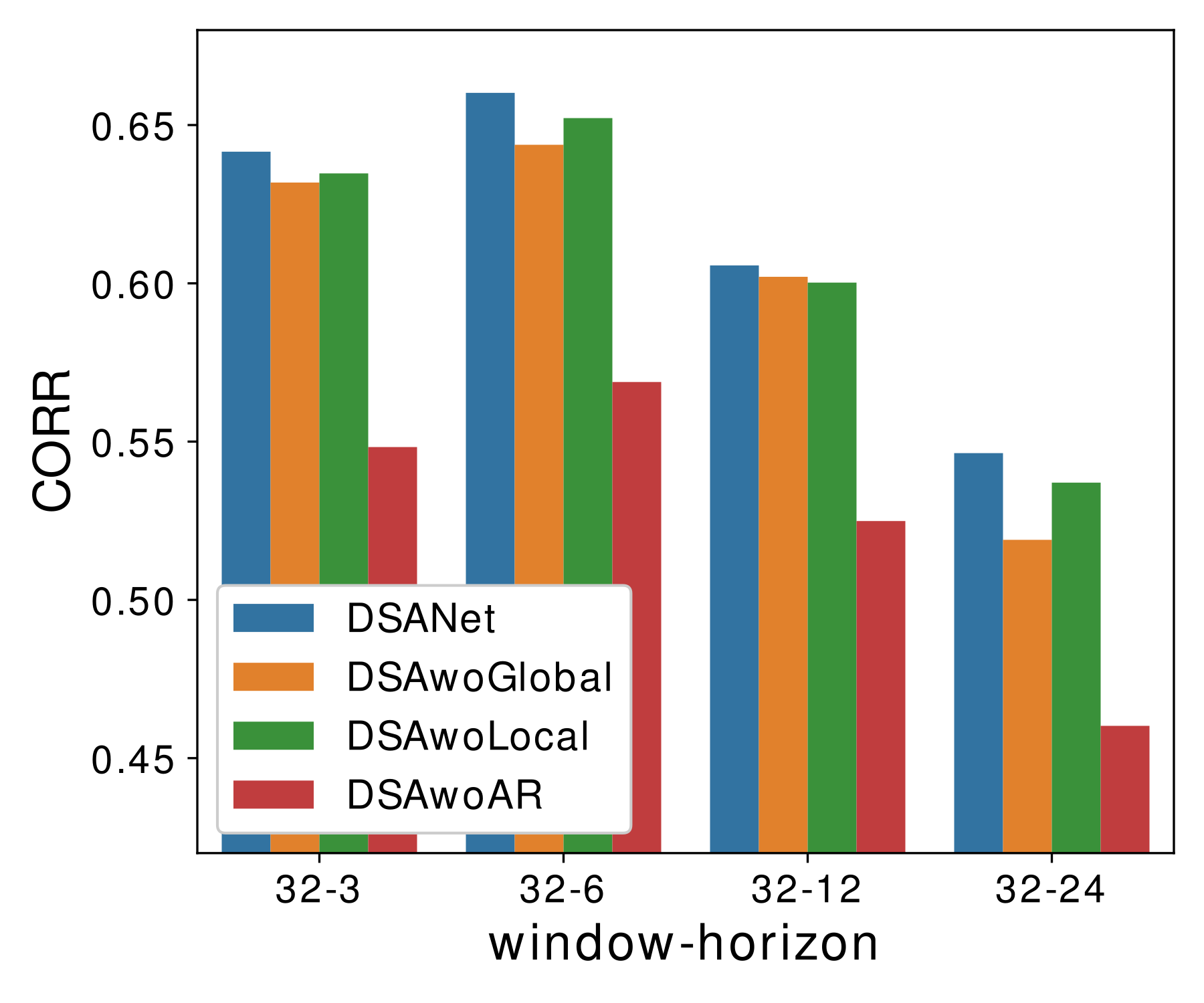
Observations:

1. The best result on each window-horizon pair is obtained by complete DSANet, showing all components have contributed to the effectiveness and robustness of the whole model.
2. The performance of DSAwoAR significantly drops, showing that the AR component plays a crucial role. The reason is that AR is generally robust to the scale changing in data according to Lai et al. (2018).
3. DSAwoGlobal and DSAwoLocal also suffer from performance loss but less than removing the AR component. This is because features learned by the two branches coincide. In other words, when one branch is removed, some of the lost features can be obtained from the other branch.

Related Work

We first consider statistical linear methods for multivariate time series. Here, the vector autoregression (VAR) model is widely considered as a baseline method, which generalizes the univariate autoregressive (AR) model by allowing for more than one evolving variable. To model non-linear relationships, some variants of the autoregressive model are used, such as LRidge, LSVR and Gaussian process (GP). However, they assume certain distribution or function form of time series and fail to capture different forms of nonlinearity.

Due to the ability to flexibly model various non-linear relationships, neural networks are often applied to enable non-linear forecasting models. For example, recurrent neural network models using LSTM or GRU are often used to provide non-linear time series forecasting. To predict more accurately, complex structures such as recurrent-skip layer (LSTNet-S), temporal attention layer (LSTNet-A) (Lai et al., 2018), and a novel temporal pattern attention mechanism (TPA) (Shih et al., 2018) have been proposed. However, when working on data with dynamic-period patterns or nonperiodic patterns, their performance drops significantly.

BibTex

If our paper and codes are helpful for you research, please cite our paper:

@inproceedings{Huang2019DSANet,
  author = {Siteng Huang and Donglin Wang and Xuehan Wu and Ao Tang},
  title = {DSANet: Dual Self-Attention Network for Multivariate Time Series Forecasting},
  booktitle = {Proceedings of the 28th {ACM} International Conference on Information and Knowledge Management},
  month = {November},
  year = {2019},
  address = {Beijing, China}
}